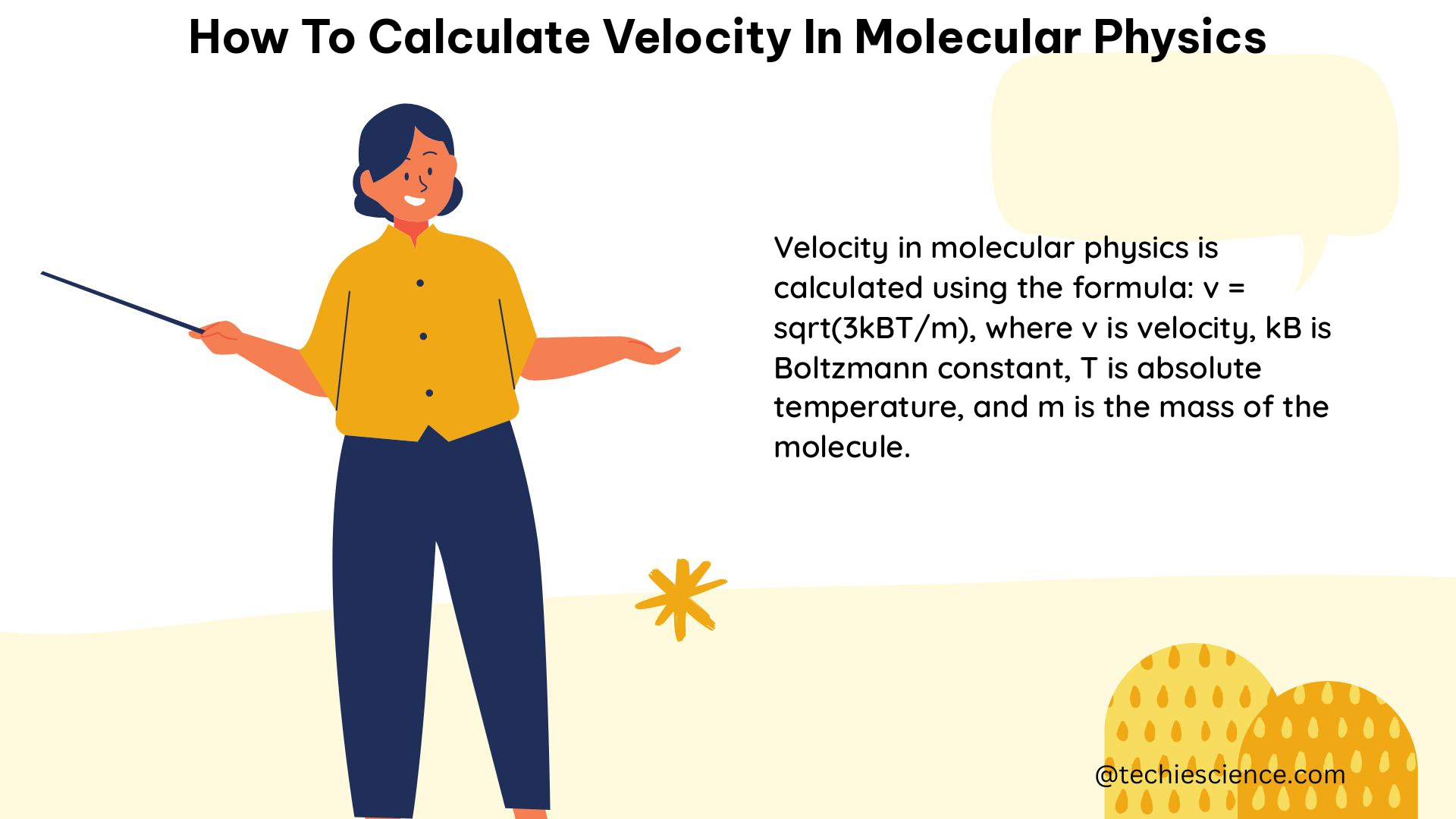
In the realm of molecular physics, understanding the concept of velocity is crucial for analyzing the behavior and dynamics of particles at the microscopic level. Velocity, a vector quantity, represents the rate of change in the position of a particle over time, and its accurate calculation is essential for various applications, from studying chemical reactions to modeling the flow of fluids. In this comprehensive guide, we will delve into the intricacies of calculating velocity in molecular physics, exploring the relevant formulas, principles, and practical considerations.
Understanding Velocity in Molecular Physics
Velocity, denoted as v, is the measure of the rate of change in the position of a particle over time. In molecular physics, particles can exhibit various types of motion, including linear, circular, and accelerated motion. To calculate velocity in these different scenarios, we need to employ specific formulas and principles.
Linear Motion
For particles moving in a straight line at a constant rate, the formula for velocity is:
v = d/t
Where:
– v is the velocity (in meters per second, m/s)
– d is the distance traveled (in meters, m)
– t is the time elapsed (in seconds, s)
This formula is applicable when the particle’s motion is linear and the speed remains constant throughout the time interval.
Circular Motion
In the case of particles moving in a circular path, the velocity is calculated by dividing the circumference of the circular path by the time period over which the particle completes one revolution. The formula for velocity in circular motion is:
v = 2πr/t
Where:
– v is the velocity (in meters per second, m/s)
– r is the radius of the circular path (in meters, m)
– t is the time period for one revolution (in seconds, s)
This formula is useful for analyzing the motion of particles in circular trajectories, such as those found in certain molecular structures or in the motion of electrons around the nucleus of an atom.
Accelerated Motion
When particles experience acceleration, the velocity changes over time. In such cases, the formula for velocity becomes:
v = v₀ + at
Where:
– v is the final velocity (in meters per second, m/s)
– v₀ is the initial velocity (in meters per second, m/s)
– a is the acceleration (in meters per second squared, m/s²)
– t is the time elapsed (in seconds, s)
This formula is applicable when the acceleration of the particle is constant throughout the time interval.
Velocity of Particles in Liquids
In the context of molecular physics, the velocity of particles in liquids is an important consideration. The formula for the velocity of particles in a liquid is given by:
v = aν = D/(ga)
Where:
– v is the velocity of the particles (in meters per second, m/s)
– a is the distance between particles in the liquid (in meters, m)
– ν is the number of times per second a particle changes places with a neighbor (in hertz, Hz)
– D is the self-diffusion coefficient of the liquid (in square meters per second, m²/s)
– g is a geometric factor (dimensionless)
This formula can be used to estimate the velocity of particles in a liquid, such as water, by using the self-diffusion coefficient and the diameter of the particles.
Relativistic Considerations
When dealing with high-speed particles in molecular physics, it is essential to consider the principles of relativistic physics. According to the theory of relativity, the mass of an object increases as its velocity approaches the speed of light. This has a significant impact on the kinetic energy of the particle.
The formula for relativistic kinetic energy is:
KErel = (γ - 1)mc²
Where:
– KErel is the relativistic kinetic energy (in joules, J)
– γ is the Lorentz factor (dimensionless)
– m is the rest mass of the object (in kilograms, kg)
– c is the speed of light (in meters per second, m/s)
At low velocities, this formula becomes the same as the classical formula for kinetic energy:
KEclass = 1/2mv²
Where:
– KEclass is the classical kinetic energy (in joules, J)
– m is the mass of the object (in kilograms, kg)
– v is the velocity of the object (in meters per second, m/s)
Understanding the principles of relativistic physics is crucial when dealing with high-speed particles in molecular physics, as it allows for accurate calculations and predictions of their behavior.
Practical Examples and Numerical Problems
To further illustrate the concepts of velocity calculation in molecular physics, let’s consider some practical examples and numerical problems.
Example 1: Linear Motion of a Molecule
Suppose a molecule travels a distance of 10 meters in 2 seconds. Calculate the velocity of the molecule.
Given:
– Distance (d) = 10 meters
– Time (t) = 2 seconds
Using the formula for linear motion:
v = d/t
v = 10 m / 2 s
v = 5 m/s
Therefore, the velocity of the molecule is 5 meters per second.
Example 2: Circular Motion of an Electron
An electron is orbiting a nucleus with a radius of 5 × 10^-10 meters. If the electron completes one revolution in 2 × 10^-16 seconds, calculate the velocity of the electron.
Given:
– Radius (r) = 5 × 10^-10 meters
– Time period (t) = 2 × 10^-16 seconds
Using the formula for circular motion:
v = 2πr/t
v = 2π × (5 × 10^-10 m) / (2 × 10^-16 s)
v = 1.57 × 10^6 m/s
Therefore, the velocity of the electron is approximately 1.57 × 10^6 meters per second.
Example 3: Accelerated Motion of a Molecule
A molecule starts with an initial velocity of 10 m/s and experiences a constant acceleration of 2 m/s². Calculate the velocity of the molecule after 5 seconds.
Given:
– Initial velocity (v₀) = 10 m/s
– Acceleration (a) = 2 m/s²
– Time (t) = 5 seconds
Using the formula for accelerated motion:
v = v₀ + at
v = 10 m/s + (2 m/s²) × (5 s)
v = 20 m/s
Therefore, the velocity of the molecule after 5 seconds is 20 meters per second.
These examples demonstrate the application of the various formulas and principles discussed in this guide to calculate the velocity of particles in different scenarios within the realm of molecular physics.
Conclusion
Calculating velocity in molecular physics is a fundamental skill that allows for the understanding and analysis of the behavior of particles at the microscopic level. By mastering the formulas and principles presented in this guide, you can effectively determine the velocity of particles in linear, circular, and accelerated motion, as well as the velocity of particles in liquids. Additionally, considering the principles of relativistic physics is crucial when dealing with high-speed particles. Through the practical examples and numerical problems provided, you can further solidify your understanding and apply these concepts to real-world scenarios in molecular physics.
References
- Velocity Calculation: https://www.wikihow.com/Calculate-Velocity
- Velocity of Particles in Liquids: https://physics.stackexchange.com/questions/111743/is-there-an-equation-to-calculate-the-average-speed-of-liquid-molecules
- Displacement, Velocity, and Time: https://www.khanacademy.org/science/physics/one-dimensional-motion/displacement-velocity-time/v/calculating-average-velocity-or-speed
- Measurable Quantities: https://www.sciencedirect.com/topics/engineering/measurable-quantity
- Relativistic Energy: https://courses.lumenlearning.com/suny-physics/chapter/28-6-relativistic-energy/

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.