Mastering the Art of Calculating Velocity from Momentum: A Comprehensive Guide

Calculating velocity from momentum is a fundamental concept in classical mechanics, and understanding this relationship is crucial for physics students and professionals alike. In this comprehensive guide, we will delve into the intricacies of this topic, providing you with a step-by-step approach to mastering the art of velocity calculation from momentum.

The Momentum-Velocity Relationship

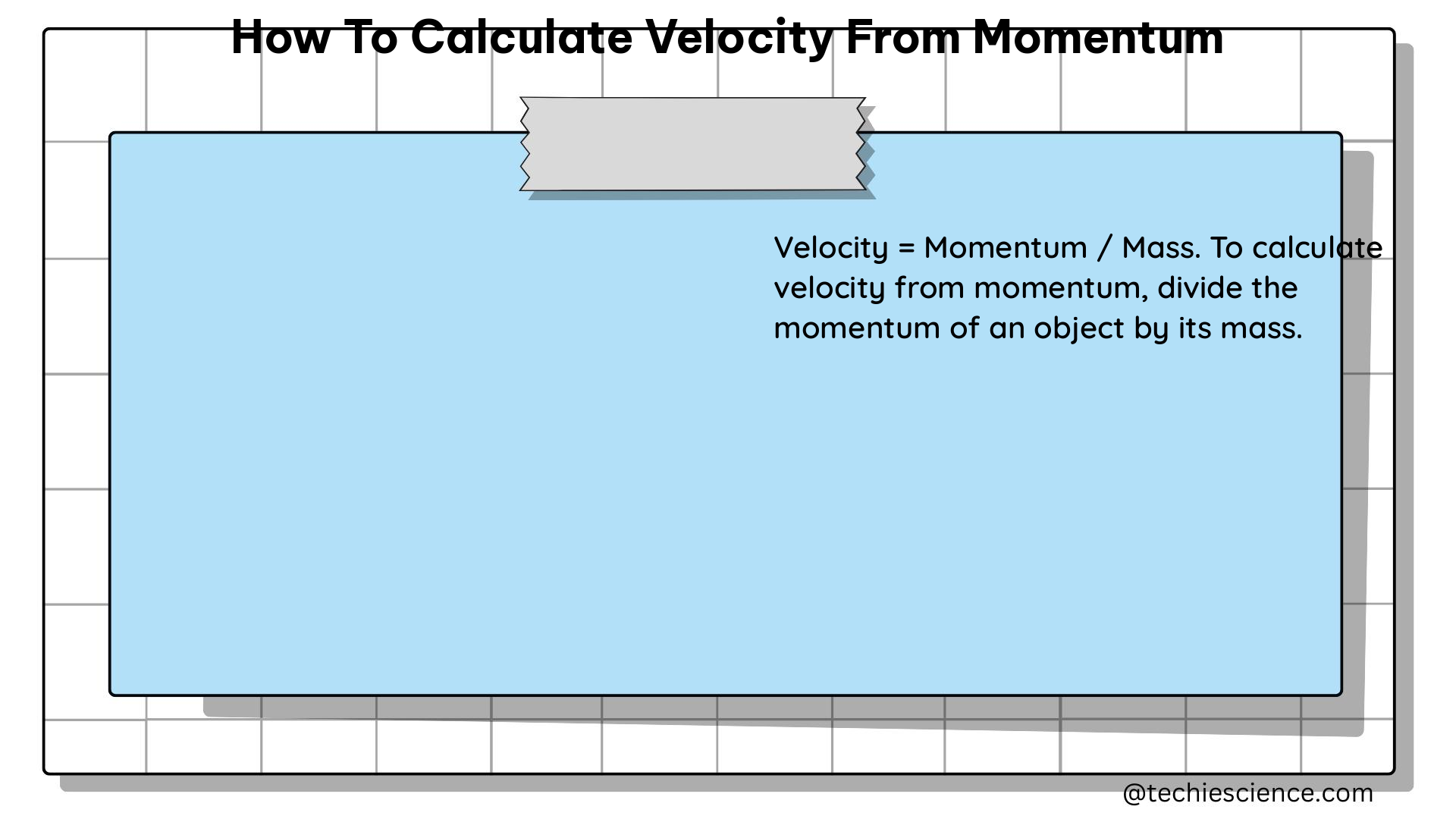
The relationship between momentum and velocity is governed by the following formula:

p = m * v

where:
– p is the momentum of the object
– m is the mass of the object
– v is the velocity of the object

Rearranging this formula, we can solve for the velocity:

v = p / m

This equation forms the foundation for calculating velocity from momentum.

Calculating Velocity for a Single Particle

To calculate the velocity of a single particle with known momentum and mass, follow these steps:

1. Identify the given values:
2. Momentum (p) of the particle

3. Mass (m) of the particle

4. Substitute the values into the formula:
   v = p / m

5. Perform the calculation to find the velocity (v).

Example:
Suppose a particle has a momentum of 10 kg·m/s and a mass of 2 kg. To calculate the velocity, we can use the formula:

v = p / m
v = 10 kg·m/s / 2 kg
v = 5 m/s

Therefore, the velocity of the particle is 5 m/s.

Calculating Velocity for a System of Particles

When dealing with a system of particles moving in arbitrary directions, the calculation of velocity becomes more complex. In this case, we need to follow these steps:

1. Calculate the magnitude of the momentum vector for each particle.
2. Resolve the momentum vector of each particle into its x- and y-components.
3. Add all of the vector components in the x direction and all of the vector components in the y direction.
4. Calculate the magnitude and direction of the total momentum vector.

Example:
Consider a system of five particles with the following momentum vectors:

Particle	Momentum (p)	Angle (θ)
1	2.1 kg·m/s	30°
2	4.2 kg·m/s	60°
3	5.2 kg·m/s	120°
4	3.4 kg·m/s	210°
5	1.6 kg·m/s	330°

To calculate the total momentum and velocity of the system, we’ll follow the steps outlined earlier:

1. Calculate the magnitude of the momentum vector for each particle:
2. p1 = 2.1 kg·m/s
3. p2 = 4.2 kg·m/s
4. p3 = 5.2 kg·m/s
5. p4 = 3.4 kg·m/s

6. p5 = 1.6 kg·m/s

7. Resolve the momentum vector of each particle into its x- and y-components:

8. p1x = 2.1 kg·m/s * cos(30°) = 1.87 kg·m/s
9. p1y = 2.1 kg·m/s * sin(30°) = 1.06 kg·m/s
10. p2x = 4.2 kg·m/s * cos(60°) = 2.12 kg·m/s
11. p2y = 4.2 kg·m/s * sin(60°) = 3.58 kg·m/s
12. p3x = 5.2 kg·m/s * cos(120°) = -2.6 kg·m/s
13. p3y = 5.2 kg·m/s * sin(120°) = 4.58 kg·m/s
14. p4x = 3.4 kg·m/s * cos(210°) = -2.75 kg·m/s
15. p4y = 3.4 kg·m/s * sin(210°) = -3.06 kg·m/s
16. p5x = 1.6 kg·m/s * cos(330°) = 0.42 kg·m/s

17. p5y = 1.6 kg·m/s * sin(330°) = -1.56 kg·m/s

18. Add all of the vector components in the x direction and all of the vector components in the y direction:

19. px = p1x + p2x + p3x + p4x + p5x = -1.55 kg·m/s

20. py = p1y + p2y + p3y + p4y + p5y = 0.54 kg·m/s

21. Calculate the magnitude and direction of the total momentum vector:

22. p = sqrt(px^2 + py^2) = 1.6 kg·m/s
23. θ = arctan(py / px) = 21°

The total momentum of the system is 1.6 kg·m/s, and it is directed at an angle of 21° relative to the positive x-axis.

To calculate the velocity of the system, we can use the formula:

v = p / m

where m is the total mass of the system. Once the total mass is known, we can substitute it into the formula to find the velocity.

Additional Considerations

• When dealing with systems of particles, it’s important to consider the conservation of momentum. The total momentum of the system remains constant unless an external force is applied.
• In some cases, the mass of the system may not be known, and you may need to calculate it using the given momentum and velocity values.
• Graphical representations, such as momentum vector diagrams, can be helpful in visualizing and understanding the momentum-velocity relationship.
• Real-world applications of momentum and velocity calculations can be found in various fields, including mechanics, engineering, and astrophysics.

Conclusion

Mastering the art of calculating velocity from momentum is a crucial skill for physics students and professionals. By understanding the fundamental relationship between these two quantities and following the step-by-step approach outlined in this guide, you can confidently tackle a wide range of problems involving momentum and velocity.

Remember to practice regularly, explore various examples, and seek further resources to deepen your understanding of this topic. With dedication and persistence, you’ll become proficient in the art of velocity calculation from momentum.

References

1. Linear Momentum and Force
2. Momentum Calculator
3. Linear Momentum and Force
4. How Can Mass Be Calculated Using Momentum and Velocity?
5. How to Calculate the Vector-Valued Momentum of a System of Particles Moving in Arbitrary Directions