How to Calculate Thermal Energy Transfer in a Heat Pump System

A heat pump is a device that transfers thermal energy from a colder environment to a warmer environment, using a refrigeration cycle. To calculate the thermal energy transfer in a heat pump system, we can use the fundamental principles of thermodynamics, specifically the first law of thermodynamics. This comprehensive guide will provide you with the necessary equations, formulas, examples, and numerical problems to help you understand and calculate the thermal energy transfer in a heat pump system.

Understanding the First Law of Thermodynamics

The first law of thermodynamics states that the total energy of an isolated system is constant; it is the conservation of energy principle. In the context of a heat pump system, the first law can be expressed as:

Qh = Qc + W

Where:
– Qh is the thermal energy transferred to the inside (warmer) environment
– Qc is the thermal energy extracted from the outside (colder) environment
– W is the work input required to operate the heat pump

This equation shows that the total thermal energy transferred to the warmer environment (Qh) is the sum of the thermal energy extracted from the colder environment (Qc) and the work input (W) required to operate the heat pump.

Calculating Thermal Energy Transfer

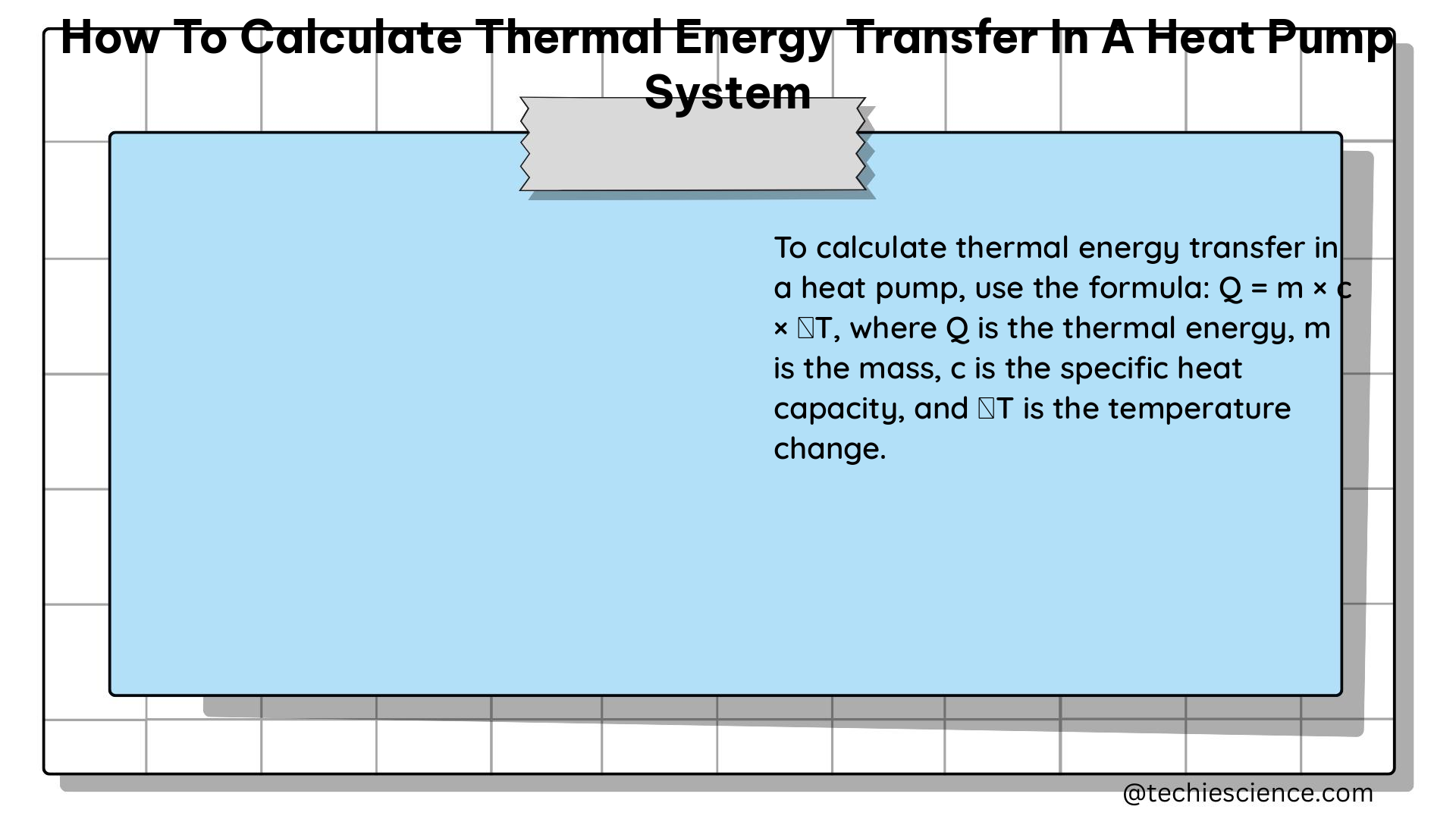
To calculate the thermal energy transfer in a heat pump system, we can use the following steps:

1. Determine the Thermal Energy Transferred to the Warmer Environment (Qh):
2. Qh can be calculated using the formula:
   Qh = m × c × ΔT

3. Where:

   • m is the mass of the warmer air (in kg)
   • c is the specific heat capacity of the warmer air (in J/kg·K)
   • ΔT is the temperature difference between the warmer air and the colder air (in K)

4. Determine the Thermal Energy Extracted from the Colder Environment (Qc):

5. Qc can be calculated using the formula:
   Qc = m × c × ΔT

6. Where:

   • m is the mass of the colder air (in kg)
   • c is the specific heat capacity of the colder air (in J/kg·K)
   • ΔT is the temperature difference between the colder air and the warmer air (in K)

7. Determine the Work Input (W):

8. W can be calculated using the formula:
   W = Qh – Qc

9. This formula is derived directly from the first law of thermodynamics equation: Qh = Qc + W

10. Calculate the Coefficient of Performance (COP):

11. The COP is a measure of the efficiency of the heat pump, and it is defined as the ratio of the thermal energy transferred to the warmer environment (Qh) to the work input (W):
    COP = Qh / W
12. A higher COP indicates a more efficient heat pump system.

Examples and Numerical Problems

Example 1:
A heat pump system is used to heat a building. The thermal energy transferred to the inside of the building (Qh) is 80 kJ, and the thermal energy extracted from the outside air (Qc) is 60 kJ. Calculate the work input (W) required to operate the heat pump.

Given:
– Qh = 80 kJ
– Qc = 60 kJ

Using the first law of thermodynamics equation:
Qh = Qc + W
W = Qh – Qc
W = 80 kJ – 60 kJ = 20 kJ

Therefore, the work input (W) required to operate the heat pump is 20 kJ.

Example 2:
A heat pump system has a COP of 3.5. If the work input (W) is 15 kJ, calculate the thermal energy transferred to the warmer environment (Qh).

Given:
– COP = 3.5
– W = 15 kJ

Using the COP formula:
COP = Qh / W
Qh = COP × W
Qh = 3.5 × 15 kJ = 52.5 kJ

Therefore, the thermal energy transferred to the warmer environment (Qh) is 52.5 kJ.

Numerical Problem:
A heat pump system is used to heat a room. The mass of the warmer air is 20 kg, and the specific heat capacity of the warmer air is 1.005 kJ/kg·K. The temperature of the warmer air is increased by 5°C. Calculate the following:
1. The thermal energy transferred to the warmer environment (Qh)
2. The thermal energy extracted from the colder environment (Qc)
3. The work input (W) required to operate the heat pump
4. The COP of the heat pump system

Given:
– m = 20 kg
– c = 1.005 kJ/kg·K
– ΔT = 5°C (or 5 K)

Step 1: Calculate the thermal energy transferred to the warmer environment (Qh)
Qh = m × c × ΔT
Qh = 20 kg × 1.005 kJ/kg·K × 5 K = 100.5 kJ

Step 2: Calculate the thermal energy extracted from the colder environment (Qc)
Qc = Qh – W
(Since we don’t know the value of W yet, we can’t calculate Qc directly. We’ll calculate it after finding the value of W.)

Step 3: Calculate the work input (W) required to operate the heat pump
W = Qh – Qc
W = 100.5 kJ – Qc

Step 4: Calculate the COP of the heat pump system
COP = Qh / W
COP = 100.5 kJ / W

Now, we can solve for Qc and W:
Qc = Qh – W
Qc = 100.5 kJ – W

COP = Qh / W
W = Qh / COP
W = 100.5 kJ / COP

Substituting the value of W in the equation for Qc:
Qc = 100.5 kJ – (100.5 kJ / COP)
Qc = 100.5 kJ × (1 – 1/COP)

Therefore, the final answers are:
1. Qh = 100.5 kJ
2. Qc = 100.5 kJ × (1 – 1/COP)
3. W = 100.5 kJ / COP
4. COP = Qh / W

These examples and numerical problems demonstrate the step-by-step process of calculating the thermal energy transfer in a heat pump system using the first law of thermodynamics and the concept of the coefficient of performance (COP).

Additional Considerations

• The performance of a heat pump system can be affected by various factors, such as the temperature difference between the warmer and colder environments, the efficiency of the compressor, and the properties of the refrigerant used.
• In practice, the actual COP of a heat pump system may be lower than the theoretical COP due to various losses and inefficiencies in the system.
• Heat pumps can also be used for cooling, where the direction of heat transfer is reversed, and the thermal energy is extracted from the warmer environment and transferred to the colder environment.
• The choice of refrigerant used in a heat pump system can have a significant impact on its efficiency and environmental impact.

Conclusion

In this comprehensive guide, we have explored the fundamental principles and equations needed to calculate the thermal energy transfer in a heat pump system. By understanding the first law of thermodynamics, the concept of COP, and working through examples and numerical problems, you should now have a solid understanding of how to calculate the thermal energy transfer in a heat pump system. This knowledge can be applied to the design, analysis, and optimization of heat pump systems in various applications.

References

1. Cengel, Y. A., & Boles, M. A. (2015). Thermodynamics: An Engineering Approach (8th ed.). McGraw-Hill Education.
2. Çengel, Y. A., & Ghajar, A. J. (2020). Heat and Mass Transfer: Fundamentals and Applications (6th ed.). McGraw-Hill Education.
3. Moran, M. J., Shapiro, H. N., Boettner, D. D., & Bailey, M. B. (2018). Fundamentals of Engineering Thermodynamics (9th ed.). Wiley.
4. Dincer, I., & Rosen, M. A. (2013). Exergy: Energy, Environment and Sustainable Development (2nd ed.). Elsevier.
5. Stoecker, W. F., & Jones, J. W. (1982). Refrigeration and Air Conditioning (2nd ed.). McGraw-Hill.