Tension force is a fundamental concept in physics and engineering that describes the pulling or stretching force in an object or system. It arises when an object is subjected to an external force that attempts to elongate or compress it. Understanding how to calculate tension force is crucial for various applications, from analyzing the stability of structures to determining the forces within complex mechanical systems.
In this blog post, we will delve into the different scenarios where tension force calculations are applicable. We will explore the formulas, equations, and step-by-step methods to calculate tension force in various situations. Through examples and explanations, we will demystify this concept and equip you with the tools to confidently calculate tension forces.
The Formula for Calculating Tension Force
The Basic Tension Force Formula

The tension force, denoted by T, can be calculated using the following formula:
![]()
Where:
– T represents the tension force.
– F is the applied force that is responsible for creating the tension.
– θ denotes the angle between the direction of the applied force and the direction of the object or system.
The sine function accounts for the component of the applied force that contributes to the tension force.
How to Use the Tension Force Formula
To use the tension force formula, follow these steps:
- Identify the applied force F and the angle θ between the force and the object or system.
- Substitute the values into the tension force formula:
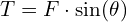 .
. - Calculate the value of T using the appropriate units.
Examples of Tension Force Calculations

Let’s consider a few examples to illustrate the calculation of tension force using the formula.
Example 1:
Suppose a person pulls a crate with a force of 50 Newtons at an angle of 30 degrees with the horizontal. To find the tension force in the rope, we can use the tension force formula:
![]()
Simplifying this equation, we find:
![]()
In this case, the tension force in the rope is 25 Newtons.
Example 2:
Consider a scenario where a cable is supporting a hanging mass with a force of 100 Newtons at an angle of 60 degrees with the vertical. By applying the tension force formula, we can determine the tension force in the cable:
![]()
Solving this equation:
![]()
Thus, the tension force in the cable is approximately 86.6 Newtons.
Calculating Tension Force in Different Scenarios
Now that we understand the basic tension force formula, let’s explore how it can be applied in various scenarios. We will discuss specific situations where tension force calculations are crucial and provide step-by-step methods for calculation.
How to Calculate Tension Force in a String
Tension force calculations in a string are relatively straightforward. The tension force in the string is equal at all points along the string, assuming it is massless and inextensible. Therefore, to calculate the tension force in a string, you can use the same tension force formula we discussed earlier.
How to Calculate Tension Force in a Cable
When dealing with cables, such as those used in suspension bridges or cranes, we can calculate the tension force by considering the forces acting on the cable. The tension force in the cable would be equal to the sum of all the forces acting on it, such as the weight of the hanging object or the external forces applied.
How to Calculate Tension Force in a Spring
In the case of a spring, the tension force is determined by Hooke’s Law, which states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position. The tension force in a spring can be calculated using the formula:
![]()
Where:
– T represents the tension force.
– k is the spring constant, which characterizes the stiffness of the spring.
– x denotes the displacement from the equilibrium position.
How to Calculate Tension Force in an Atwood Machine
An Atwood machine involves two masses connected by a string or a rope passing over a pulley. The tension force in such a system can be calculated by considering the difference in masses and the acceleration of the system. The formula to calculate tension force in an Atwood machine is dependent on the specific configuration and can be derived using Newton’s second law and the principles of equilibrium.
How to Calculate Tension Force on an Inclined Plane
When an object is placed on an inclined plane and connected to a string, the tension force in the string can be calculated by considering the forces acting on the object. By analyzing the forces along the inclined plane, including the component of the weight parallel to the plane, the tension force can be determined.
How to Calculate Tension Force of a Hanging Mass
When a mass is hanging vertically from a string or a cable, the tension force in the string can be calculated by considering the weight of the mass and the acceleration due to gravity. The tension force will be equal to the weight of the mass.
How to Calculate Tension Force Between Two Objects
In situations where two objects are connected by a string or a cable, the tension force can be calculated by considering the forces acting on each object. By analyzing the forces involved, including the weight of the objects and any external forces applied, the tension force can be determined.
How to Calculate Tension Force in a Pulley System
Pulley systems are commonly used in mechanical systems to transmit forces and change the direction of motion. To calculate the tension force in a pulley system, you need to consider the masses involved, the number of pulleys, and any external forces applied. The equations for calculating tension forces in pulley systems can be derived using Newton’s second law and the principles of equilibrium.
How to Calculate Tension Force with Friction
When friction is present in a system, such as a block sliding on a surface with a tension force, the calculation of tension force becomes more complex. In such cases, you need to consider the forces due to friction and the normal force acting on the object. The tension force can be determined by analyzing the forces involved and applying the appropriate equations.
How to Calculate Tension Force at an Angle

When the tension force is applied at an angle to the direction of the object or system, the tension force formula we discussed earlier can be used. By considering the magnitude of the applied force and the angle between the force and the object, the tension force can be calculated.
How to Calculate Tension Force in Circular Motion
In situations involving circular motion, such as a mass rotating in a horizontal circle connected by a string or a cable, the tension force can be calculated by considering the centripetal force required to keep the object in circular motion. By equating the tension force with the centripetal force, the tension force can be determined.
Worked Out Examples
Let’s now work through some examples to solidify our understanding of tension force calculations in different scenarios.
Example of Calculating Tension Force in a String
Suppose we have a string connecting two objects with masses of 5 kg and 8 kg. The objects are hanging vertically, and we want to calculate the tension force in the string. We know that the acceleration due to gravity is 9.8 m/s².
To calculate the tension force, we need to consider the weight of each object. The tension force will be equal to the sum of the weights of the objects:
![]()
Substituting the given values:
![]()
![]()
![]()
Therefore, the tension force in the string is 127.4 Newtons.
Example of Calculating Tension Force on an Inclined Plane
Consider an object with a mass of 10 kg placed on an inclined plane with an angle of 30 degrees. The object is connected to a string, and we want to calculate the tension force in the string. Given that the acceleration due to gravity is 9.8 m/s², we can determine the tension force.
To calculate the tension force, we need to consider the forces acting on the object. These forces include the component of the weight parallel to the inclined plane and the normal force. By analyzing the forces, we can find the tension force:
![]()
Substituting the given values:
![]()
![]()
![]()
Therefore, the tension force in the string is 49 Newtons.
Example of Calculating Tension Force in a Pulley System
Let’s consider a pulley system with two masses connected by a rope passing over the pulley. The first mass has a weight of 5 kg, while the second mass has a weight of 8 kg. We want to calculate the tension force in the rope.
To calculate the tension force, we need to consider the forces acting on each mass. The tension force in the rope will be equal at both ends, so we can set up the following equations:
![]()
![]()
Since the tension force is equal at both ends, we can equate the two equations:
![]()
Simplifying the equation, we find:
![]()
This equation is not possible, indicating that there is no solution. In this case, the tension force in the pulley system cannot be determined without additional information.
Example of Calculating Tension Force with Friction
Suppose we have a block of mass 2 kg sliding on a horizontal surface. The block is connected to a string, and a tension force of 10 Newtons is applied at an angle of 30 degrees with the horizontal. The coefficient of friction between the block and the surface is 0.2. We want to calculate the tension force in the string.
To calculate the tension force, we need to consider the forces acting on the block. These forces include the tension force, the weight of the block, and the force of friction. By analyzing the forces, we can determine the tension force:
![]()
Where:
– T is the tension force.
– f_f represents the force of friction.
– m is the mass of the block.
– a is the acceleration of the block.
We can calculate the force of friction using the equation:
![]()
Where:
– μ is the coefficient of friction.
– N represents the normal force.
Since the block is on a horizontal surface, the normal force is equal to the weight of the block:
![]()
Substituting the values, we find:
![]()
![]()
Now we can calculate the force of friction:
![]()
![]()
Next, we can calculate the acceleration of the block:
![]()
![]()
Finally, we can solve for the tension force:
![]()
![]()
![]()
![]()
Therefore, the tension force in the string is 6.08 Newtons.
Example of Calculating Tension Force at an Angle

Consider a situation where an object of mass 5 kg is hanging from a string at an angle of 45 degrees with the vertical. We want to calculate the tension force in the string.
To calculate the tension force, we can use the tension force formula we discussed earlier:
![]()
Substituting the given values:
![]()
![]()
![]()
Therefore, the tension force in the string is approximately 34.3 Newtons.
In this blog post, we have explored the concept of tension force and how to calculate it in various scenarios. We began with the basic tension force formula, which considers the applied force and its angle of application. We then delved into specific scenarios, such as tension force in strings, cables, springs, pulley systems, and more. Through examples and step-by-step calculations, we have demonstrated how to determine tension forces accurately.
Understanding tension force and its calculations is essential for engineers, physicists, and anyone dealing with mechanical systems. By mastering these concepts and formulas, you will be better equipped to analyze and design structures, machines, and systems that rely on tension forces. So, the next time you encounter a situation involving tension forces, you’ll feel confident in calculating them accurately.
Numerical Problems on how to calculate tension force
Problem 1:
A rope of length 10 meters is tied to a support at one end and a block of mass 5 kg is attached to the other end. The block is being pulled horizontally with a force of 20 N. Calculate the tension force in the rope.
Solution:
Given:
Length of the rope, ![]()
Mass of the block, ![]()
Force being applied, ![]()
To calculate the tension force in the rope, we can use the equation:
![]()
Where:
![]() is the tension force,
is the tension force,
![]() is the applied force,
is the applied force,
![]() is the mass of the block, and
is the mass of the block, and
![]() is the acceleration due to gravity.
is the acceleration due to gravity.
Substituting the given values:
![]()
Simplifying:
![]()
![]()
Therefore, the tension force in the rope is 69 N.
Problem 2:
A block of mass 2 kg is suspended by two ropes as shown in the figure. Find the tension forces in ropes A and B.
![]() (https://i.imgur.com/HG9jXPZ.png)
(https://i.imgur.com/HG9jXPZ.png)
Solution:
Let’s consider the tension force in rope A as ![]() and the tension force in rope B as
and the tension force in rope B as ![]() .
.
For equilibrium, the sum of the forces in the vertical direction should be zero.
![]()
Similarly, the sum of the forces in the horizontal direction should also be zero.
![]()
We can solve these two equations simultaneously to find the values of ![]() and
and ![]() .
.
Simplifying the equation for the vertical direction:
![]()
Simplifying the equation for the horizontal direction:
![]()
We can solve these equations to find the values of ![]() and
and ![]() .
.
Problem 3:
A 10 kg mass is suspended from a vertical rope. Find the minimum tension force in the rope required to keep the mass stationary.
Solution:
When the mass is stationary, the tension force in the rope should balance the weight of the mass.
Let’s assume the tension force in the rope is ![]() . The weight of the mass is given by
. The weight of the mass is given by ![]() , where
, where ![]() is the mass and
is the mass and ![]() is the acceleration due to gravity.
is the acceleration due to gravity.
For the mass to be stationary, the tension force should be equal to the weight of the mass:
![]()
Substituting the given values:
![]()
Simplifying:
![]()
Therefore, the minimum tension force in the rope required to keep the mass stationary is 98 N.
I am Keerthi K Murthy, I have completed post graduation in Physics, with the specialization in the field of solid state physics. I have always consider physics as a fundamental subject which is connected to our daily life. Being a science student I enjoy exploring new things in physics. As a writer my goal is to reach the readers with the simplified manner through my articles.