How to Calculate Speed: A Comprehensive Guide for Physics Students

Summary

Speed is a fundamental concept in physics that describes the rate at which an object covers distance over time. Calculating speed is essential for understanding various physical phenomena, from the motion of objects to the performance of vehicles. This comprehensive guide will provide you with a detailed understanding of the formulas, principles, and practical applications of speed calculations.

Understanding Speed

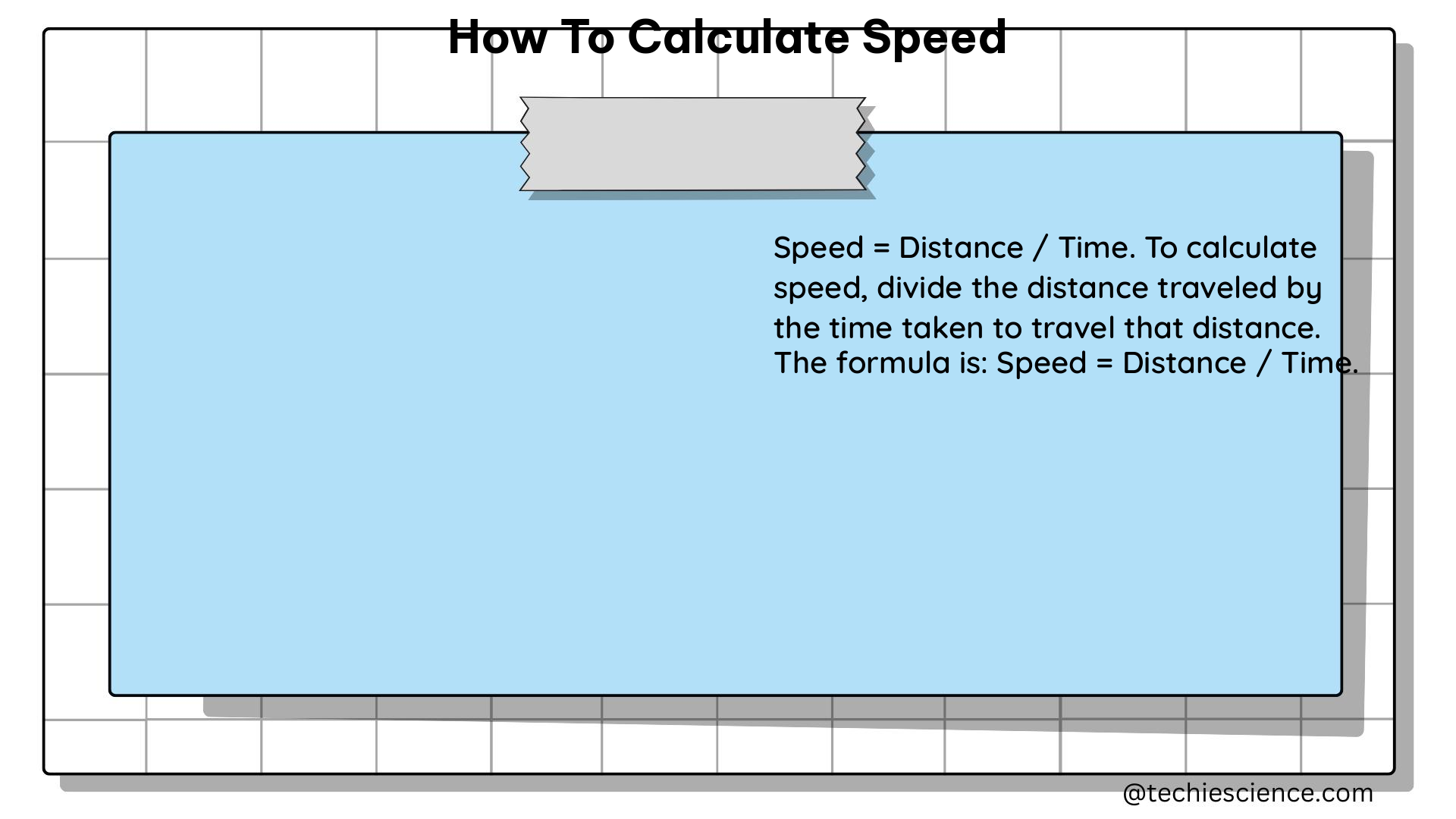
Speed is a scalar quantity, meaning it has a magnitude (numerical value) but no direction. It is typically represented by the symbol “v” and is calculated by dividing the distance traveled by the time taken. The formula for calculating speed is:

v = s/t

where:
– v is the speed
– s is the distance traveled
– t is the time taken

Average Speed

When an object’s speed varies over a given time interval, we can calculate its average speed using the formula:

v_avg = Δs/Δt

where:
– v_avg is the average speed
– Δs is the change in distance
– Δt is the change in time

Instantaneous Speed

Instantaneous speed is the speed of an object at a specific moment in time. It is calculated using the formula:

v = ds/dt

where:
– v is the instantaneous speed
– ds is the infinitesimal change in distance
– dt is the infinitesimal change in time

Instantaneous speed is often measured using instruments like speedometers, which provide a real-time reading of an object’s speed.

Calculating Speed in Different Scenarios

Linear Motion

When an object is moving in a straight line, the speed can be calculated using the formula:

v = s/t

For example, if a car travels a distance of 200 miles in 4 hours, its average speed would be:

v = 200 miles / 4 hours = 50 miles/hour

Circular Motion

When an object is moving in a circular path, its speed can be calculated using the formula:

v = 2πr/t

where:
– v is the speed
– r is the radius of the circular path
– t is the time taken to complete one revolution

For instance, if a merry-go-round has a radius of 5 meters and completes one revolution every 10 seconds, its speed would be:

v = 2π × 5 m / 10 s = 3.14 m/s

Rotational Motion

In rotational motion, the speed is often expressed in terms of angular velocity, which is the rate of change of the object’s angular position. The formula for calculating angular velocity is:

ω = Δθ/Δt

where:
– ω is the angular velocity
– Δθ is the change in angular position
– Δt is the change in time

The linear speed of a point on the rotating object can then be calculated using the formula:

v = ωr

where:
– v is the linear speed
– ω is the angular velocity
– r is the distance from the point to the axis of rotation

For example, if a fan blade rotates at 1200 revolutions per minute (RPM) and has a radius of 0.5 meters, its linear speed would be:

ω = 1200 RPM × 2π rad/rev / 60 s/min = 125.66 rad/s
v = 125.66 rad/s × 0.5 m = 62.83 m/s

Relative Speed

When two objects are moving relative to each other, their relative speed can be calculated using the formula:

v_rel = v_1 – v_2

where:
– v_rel is the relative speed
– v_1 is the speed of the first object
– v_2 is the speed of the second object

For instance, if a car is traveling at 80 km/h and a motorcycle is traveling at 60 km/h in the same direction, the relative speed between them would be:

v_rel = 80 km/h – 60 km/h = 20 km/h

Factors Affecting Speed Calculations

When calculating speed, it is important to consider the following factors:

1. Accuracy of Measurements: Precise measurements of distance and time are crucial for accurate speed calculations. Errors in these measurements can significantly impact the final result.

2. Units and Conversions: Speed can be expressed in various units, such as meters per second (m/s), kilometers per hour (km/h), or miles per hour (mph). Ensure that you use the appropriate units and perform any necessary conversions.

3. Direction of Motion: In the case of vector quantities like velocity, the direction of motion must be taken into account. This is particularly important when dealing with relative motion or circular motion.

4. External Forces: External forces, such as friction, air resistance, or gravity, can affect the speed of an object. These forces should be considered when analyzing the motion of an object.

5. Acceleration and Deceleration: If an object’s speed is changing over time, you may need to use more advanced formulas, such as those involving acceleration or deceleration, to calculate its speed accurately.

Practical Applications of Speed Calculations

Speed calculations have numerous practical applications in various fields, including:

1. Transportation: Calculating the speed of vehicles, such as cars, trains, or airplanes, is essential for transportation planning, safety, and performance analysis.

2. Sports and Athletics: Speed calculations are crucial in sports, where athletes’ performance is often measured in terms of speed, such as in running, cycling, or motorsports.

3. Engineering and Manufacturing: Speed calculations are used in the design and optimization of machinery, such as turbines, motors, or conveyor belts, to ensure efficient and safe operation.

4. Physics and Astronomy: Speed calculations are fundamental in the study of various physical phenomena, from the motion of celestial bodies to the propagation of waves and the behavior of subatomic particles.

5. Everyday Life: Understanding speed calculations can be helpful in everyday situations, such as estimating travel times, understanding the performance of household appliances, or analyzing the motion of objects in our daily lives.

Conclusion

Calculating speed is a fundamental skill in physics that has numerous practical applications. By understanding the formulas, principles, and factors involved in speed calculations, you can develop a deeper understanding of the physical world and solve a wide range of problems. This comprehensive guide has provided you with the necessary knowledge and tools to become proficient in calculating speed, whether you are a physics student, an engineer, or simply someone interested in the science of motion.

References

1. How to Calculate Speed and Distance – GeeksforGeeks
2. Calculate Speed, Distance and Time – Programiz
3. Speed, Velocity and Acceleration – Physics Classroom
4. Speed and Velocity – Khan Academy
5. Speed, Velocity and Acceleration – Flinn Scientific