How to Calculate Projectile Motion: A Comprehensive Guide

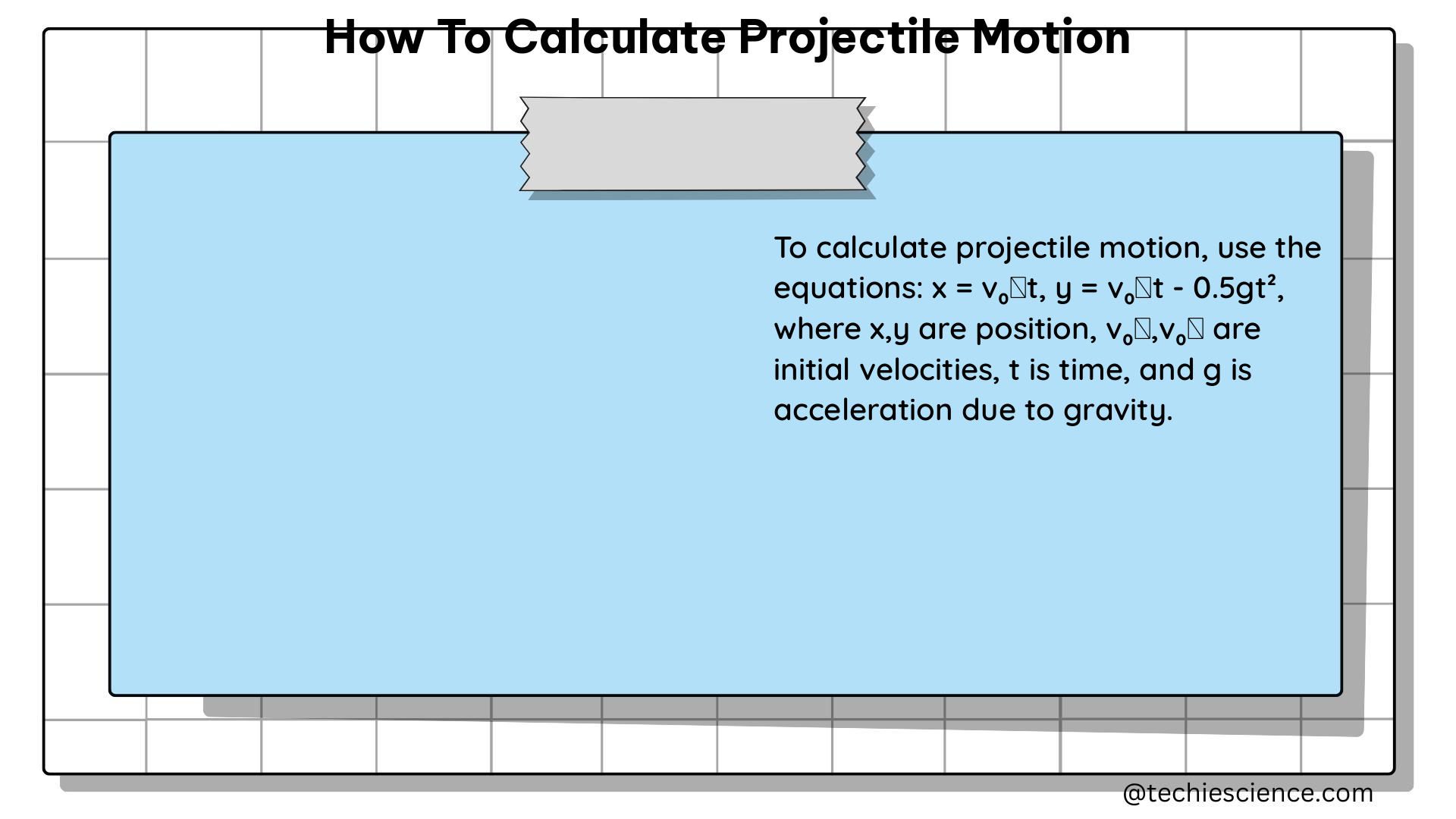
Projectile motion is a fundamental concept in physics that describes the motion of an object that is launched into the air and subjected to the constant acceleration of gravity. To accurately calculate various aspects of projectile motion, such as the time of flight, range, and maximum height, you can use a set of equations derived from the principles of kinematics and the constant acceleration due to gravity.

Understanding the Equations of Projectile Motion

The key equations used to calculate projectile motion are as follows:

1. Horizontal Velocity Component (Vx):
2. Equation: Vx = V₀ cos(α)

3. Where:

   • Vx is the horizontal velocity component
   • V₀ is the initial velocity
   • α is the launch angle

4. Vertical Velocity Component (Vy):

5. Equation: Vy = V₀ sin(α) – gt

6. Where:

   • Vy is the vertical velocity component
   • V₀ is the initial velocity
   • α is the launch angle
   • g is the acceleration due to gravity (9.8 m/s²)
   • t is the time

7. Time of Flight (t):

8. If the initial height (h) is 0:
   • Equation: t = 2Vy₀/g

9. If the initial height (h) is greater than 0:

   • Equation: t = [Vy₀ + √(Vy₀²+ 2gh)]/g

10. Range of the Projectile (R):

11. If the initial height (h) is 0:
    • Equation: R = 2VxVy₀/g

12. If the initial height (h) is greater than 0:

    • Equation: R = Vx[Vy₀ + √(Vy₀²+ 2gh)]/g

13. Maximum Height (hmax):

14. If the initial height (h) is 0:
    • Equation: hmax = Vy₀²/(2g)
15. If the initial height (h) is greater than 0:
    • Equation: hmax = h + Vy₀²/(2g)

In these equations, the following variables are used:
– V₀: Initial velocity
– α: Launch angle
– g: Acceleration due to gravity (9.8 m/s²)
– t: Time
– h: Initial height
– Vx: Horizontal velocity component
– Vy: Vertical velocity component
– R: Range of the projectile
– hmax: Maximum height of the projectile

Understanding Vectors and Right Triangles

To calculate the horizontal and vertical velocity components, it is essential to understand the concepts of vectors and right triangles. The initial velocity (V₀) can be represented as a vector, and the horizontal and vertical components can be determined using trigonometric functions.

The horizontal velocity component (Vx) is equal to the initial velocity (V₀) multiplied by the cosine of the launch angle (α):
– Vx = V₀ cos(α)

The vertical velocity component (Vy) is equal to the initial velocity (V₀) multiplied by the sine of the launch angle (α), minus the product of the acceleration due to gravity (g) and the time (t):
– Vy = V₀ sin(α) – gt

By understanding these vector relationships and applying the appropriate trigonometric functions, you can accurately calculate the horizontal and vertical velocity components.

Practical Examples and Numerical Problems

To better understand the application of these equations, let’s consider some practical examples and numerical problems.

Example 1: Projectile Launched from Ground Level
Suppose a projectile is launched from ground level (h = 0) with an initial velocity of 50 m/s and a launch angle of 30 degrees. Calculate the time of flight, range, and maximum height of the projectile.

Given:
– V₀ = 50 m/s
– α = 30 degrees
– h = 0

Step 1: Calculate the horizontal velocity component (Vx).
Vx = V₀ cos(α)
Vx = 50 m/s × cos(30°) = 43.30 m/s

Step 2: Calculate the vertical velocity component (Vy).
Vy = V₀ sin(α) – gt
Vy = 50 m/s × sin(30°) – (9.8 m/s²) × t

Step 3: Calculate the time of flight (t).
Since the initial height (h) is 0, the time of flight is given by:
t = 2Vy₀/g
t = 2 × (50 m/s × sin(30°)) / 9.8 m/s² = 2.04 s

Step 4: Calculate the range (R).
Since the initial height (h) is 0, the range is given by:
R = 2VxVy₀/g
R = 2 × (43.30 m/s) × (50 m/s × sin(30°)) / 9.8 m/s² = 86.60 m

Step 5: Calculate the maximum height (hmax).
Since the initial height (h) is 0, the maximum height is given by:
hmax = Vy₀²/(2g)
hmax = (50 m/s × sin(30°))²/(2 × 9.8 m/s²) = 31.63 m

Example 2: Projectile Launched from a Non-Zero Initial Height
Suppose a projectile is launched from a height of 5 meters with an initial velocity of 60 m/s and a launch angle of 45 degrees. Calculate the time of flight, range, and maximum height of the projectile.

Given:
– V₀ = 60 m/s
– α = 45 degrees
– h = 5 m

Step 1: Calculate the horizontal velocity component (Vx).
Vx = V₀ cos(α)
Vx = 60 m/s × cos(45°) = 42.43 m/s

Step 2: Calculate the vertical velocity component (Vy).
Vy = V₀ sin(α) – gt
Vy = 60 m/s × sin(45°) – (9.8 m/s²) × t

Step 3: Calculate the time of flight (t).
Since the initial height (h) is greater than 0, the time of flight is given by:
t = [Vy₀ + √(Vy₀²+ 2gh)]/g
t = [60 m/s × sin(45°) + √((60 m/s × sin(45°))² + 2 × 9.8 m/s² × 5 m)]/9.8 m/s² = 4.24 s

Step 4: Calculate the range (R).
Since the initial height (h) is greater than 0, the range is given by:
R = Vx[Vy₀ + √(Vy₀²+ 2gh)]/g
R = (42.43 m/s) × [60 m/s × sin(45°) + √((60 m/s × sin(45°))² + 2 × 9.8 m/s² × 5 m)]/9.8 m/s² = 120.00 m

Step 5: Calculate the maximum height (hmax).
Since the initial height (h) is greater than 0, the maximum height is given by:
hmax = h + Vy₀²/(2g)
hmax = 5 m + (60 m/s × sin(45°))²/(2 × 9.8 m/s²) = 35.63 m

These examples demonstrate the application of the projectile motion equations and the importance of considering the initial height in the calculations.

Additional Considerations and Factors

When calculating projectile motion, there are a few additional factors and considerations to keep in mind:

1. Air Resistance: In real-world scenarios, air resistance can have a significant impact on the motion of a projectile. The equations presented in this guide assume negligible air resistance, but in some cases, it may be necessary to incorporate air resistance into the calculations.

2. Angle of Elevation: The angle of elevation, which is the angle between the horizontal and the line of sight to the target, can also affect the projectile’s trajectory and range.

3. Coriolis Effect: For long-range projectiles, the Coriolis effect, which is the apparent deflection of moving objects due to the Earth’s rotation, may need to be considered.

4. Projectile Shape and Drag Coefficient: The shape and aerodynamic properties of the projectile can influence its motion, and the drag coefficient should be taken into account for more accurate calculations.

5. Environmental Factors: Factors such as wind, temperature, and humidity can also affect the projectile’s motion and should be considered in certain applications.

By understanding these additional factors and incorporating them into the calculations, you can further refine your understanding of projectile motion and improve the accuracy of your predictions.

Conclusion

Calculating projectile motion is a fundamental skill in physics and can be applied in various fields, from ballistics and sports to engineering and astronomy. By mastering the equations and concepts presented in this guide, you can accurately determine the time of flight, range, and maximum height of a projectile, given the initial conditions.

Remember to always consider the initial height, understand the relationships between vectors and right triangles, and be aware of any additional factors that may influence the projectile’s motion. With practice and a solid understanding of the underlying principles, you can become proficient in calculating projectile motion and apply these skills to a wide range of real-world scenarios.

References

1. Projectile Motion – University Physics Volume 1, https://pressbooks.bccampus.ca/universityphysicssandbox/chapter/projectile-motion/
2. Projectile Motion Calculator, https://www.omnicalculator.com/physics/projectile-motion
3. Physics 223 General Physics Lab Experiment 5: Projectile Motion, https://www.phy.olemiss.edu/lab/LabPDFs/223/LabManual/5_ProjectileMotion_223/TAP_Projectiles_223.pdf
4. Projectile Motion: Equations and Examples, https://www.thoughtco.com/projectile-motion-equations-2698949
5. Projectile Motion: Theory and Examples, https://www.physicsclassroom.com/class/vectors/Lesson-4/Projectile-Motion-Theory-and-Examples