How to Calculate Mechanical Energy: A Comprehensive Guide for Beginners

Mechanical energy refers to the energy possessed by an object due to its motion or position. It is the sum of the object’s kinetic energy and potential energy. In this blog post, we will explore how to calculate mechanical energy, step-by-step. We will also delve into advanced concepts and special cases related to mechanical energy calculations. So, let’s get started!

How to Calculate Mechanical Energy

The Formula for Mechanical Energy

To calculate mechanical energy, we need to consider both kinetic energy and potential energy. The formula for mechanical energy is:

$E = KE + PE$

where $E$ is the mechanical energy, $KE$ is the kinetic energy, and $PE$ is the potential energy.

Step-by-step Guide on How to Calculate Mechanical Energy

Let’s break down the process of calculating mechanical energy into simple steps:

Determine the mass $(m$ ) of the object in question. Mass is a measure of the amount of matter an object contains.
Calculate the velocity $(v$ ) of the object. Velocity is the rate of change of an object’s position with respect to time.
Use the formula for kinetic energy to find the kinetic energy 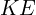$(KE$ ) of the object. The formula for kinetic energy is:

$KE = frac{1}{2}mv^2$

where $frac{1}{2}$ is a constant and $v^2$ represents the square of the velocity.

Determine the height 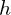$(h$ ) of the object from a reference point. Height is a measure of the object’s position relative to the ground or another reference level.
Calculate the potential energy 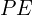$(PE$ ) of the object using the formula:

$PE = mgh$

where is the acceleration due to gravity is the mass of the object.

Finally, add the kinetic energy and potential energy together to obtain the mechanical energy 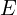$(E$ ) of the object.

Let’s illustrate this calculation with an example.

Worked-out Examples on Calculating Mechanical Energy

Example 1:

Suppose we have a ball with a mass of 2 kg and a velocity of 4 m/s. The ball is at a height of 10 meters from the ground. Let’s calculate the mechanical energy of the ball.

Mass $(m$ ) = 2 kg
Velocity $(v$ ) = 4 m/s
Height $(h$ ) = 10 m

First, let’s calculate the kinetic energy using the formula:

$KE = frac{1}{2}mv^2$

Substituting the values into the formula:

$KE = frac{1}{2} times 2 times (4)^2 = 16 text{ J}$

Next, let’s calculate the potential energy using the formula:

$PE = mgh$

Substituting the values into the formula:

$PE = 2 times 9.8 times 10 = 196 text{ J}$

Finally, let’s calculate the mechanical energy by adding the kinetic energy and potential energy together:

$E = KE + PE = 16 + 196 = 212 text{ J}$

Therefore, the mechanical energy of the ball is 212 J.

Now, let’s move on to advanced concepts in mechanical energy calculation.

Advanced Concepts in Mechanical Energy Calculation

How to Calculate Mechanical Energy without Kinetic Energy

In certain situations, we may need to calculate mechanical energy without knowing the kinetic energy. In such cases, we can use the formula for potential energy alone. This is applicable when an object is at rest or stationary. The formula for mechanical energy without kinetic energy is:

$E = PE$

How to Calculate Mechanical Energy without Mass

Sometimes, we may not have the mass of an object but still need to calculate its mechanical energy. In these situations, we can’t directly calculate the mechanical energy. However, if we know the kinetic energy and potential energy of the object, we can use the formulas mentioned earlier to find the mechanical energy.

How to Calculate Mechanical Energy without Velocity

Similar to calculating mechanical energy without mass, if we don’t have the velocity of an object but still need to find its mechanical energy, we can use the formulas for potential energy and kinetic energy to calculate it indirectly.

How to Calculate Change in Mechanical Energy

how to calculate mechanical energy — Image by Steve Zavari – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

To calculate the change in mechanical energy, we can subtract the initial mechanical energy from the final mechanical energy. The formula for change in mechanical energy is:

$Delta E = E_{text{final}} - E_{text{initial}}$

where $Delta E$ represents the change in mechanical energy, $E_{text{final}}$ is the final mechanical energy, and $E_{text{initial}}$ is the initial mechanical energy.

Now, let’s explore some special cases related to mechanical energy calculation.

Special Cases in Mechanical Energy Calculation

How to Calculate Mechanical Energy Lost due to Friction

Friction is a force that opposes motion and can cause mechanical energy to be lost. When calculating mechanical energy lost due to friction, we need to consider the work done against friction. The formula for calculating mechanical energy lost due to friction is:

$E_{text{lost}} = text{Work done against friction}$

How to Calculate Mechanical Energy Dissipated

Mechanical energy can also be dissipated or transformed into other forms, such as heat energy or sound energy. To calculate the mechanical energy dissipated, we need to consider the energy transformed or lost during the process. The formula for calculating mechanical energy dissipated depends on the specific scenario and the type of energy transformation involved.

How to Calculate Mechanical Energy Lost in a Collision

In a collision or impact, mechanical energy can be lost due to deformation or other factors. To calculate the mechanical energy lost in a collision, we need to consider the initial mechanical energy and the final mechanical energy after the collision. The formula for calculating mechanical energy lost in a collision is:

$E_{text{lost}} = E_{text{initial}} - E_{text{final}}$

where $E_{text{lost}}$ represents the mechanical energy lost, $E_{text{initial}}$ is the initial mechanical energy, and $E_{text{final}}$ is the final mechanical energy.

Numerical Problems on how to calculate mechanical energy

Image by Cristian Quinzacara – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

Problem 1:

A block of mass 2 kg is dropped from a height of 10 m. Calculate the mechanical energy of the block when it hits the ground. Assume there is no air resistance.

Solution:
Given:
Mass of the block, m = 2 kg
Height, h = 10 m

The mechanical energy of the block is given by the sum of its potential energy and kinetic energy:

Potential energy, PE = mgh
Kinetic energy, KE = 0.5mv^2

Since the block is dropped, it initially has no velocity. Therefore, its initial kinetic energy is zero.

When the block hits the ground, all of its potential energy is converted into kinetic energy. Hence, the mechanical energy is equal to the final kinetic energy.

Let’s calculate the potential energy first:

$PE = mgh = 2 times 9.8 times 10 = 196 , text{J}$

The mechanical energy of the block when it hits the ground is 196 J.

Problem 2:

A spring with a spring constant of 100 N/m is compressed by 0.1 m. Calculate the mechanical energy stored in the spring.

Solution:
Given:
Spring constant, k = 100 N/m
Compression, x = 0.1 m

The mechanical energy stored in the spring is given by the formula:

$ME = frac{1}{2} kx^2$

Substituting the given values:

$ME = frac{1}{2} times 100 times (0.1)^2 = 0.5 , text{J}$

The mechanical energy stored in the spring is 0.5 J.

Problem 3:

A car of mass 1000 kg is moving with a velocity of 20 m/s. Calculate its mechanical energy.

Solution:
Given:
Mass of the car, m = 1000 kg
Velocity, v = 20 m/s

The mechanical energy of the car is given by the sum of its kinetic energy and potential energy:

Potential energy, PE = 0 (assuming the car is at the ground level)
Kinetic energy, KE = 0.5mv^2

Substituting the given values:

$KE = 0.5 times 1000 times (20)^2 = 200,000 , text{J}$

The mechanical energy of the car is 200,000 J.

Core SME lambdageeks.com

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.

All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.

lambdageeks.com