Calculating the magnetic energy stored in an inductor is a fundamental concept in electrical engineering and physics. This comprehensive guide will provide you with a deep understanding of the underlying principles, formulas, and practical examples to help you master this essential skill.
Understanding Magnetic Energy in Inductors
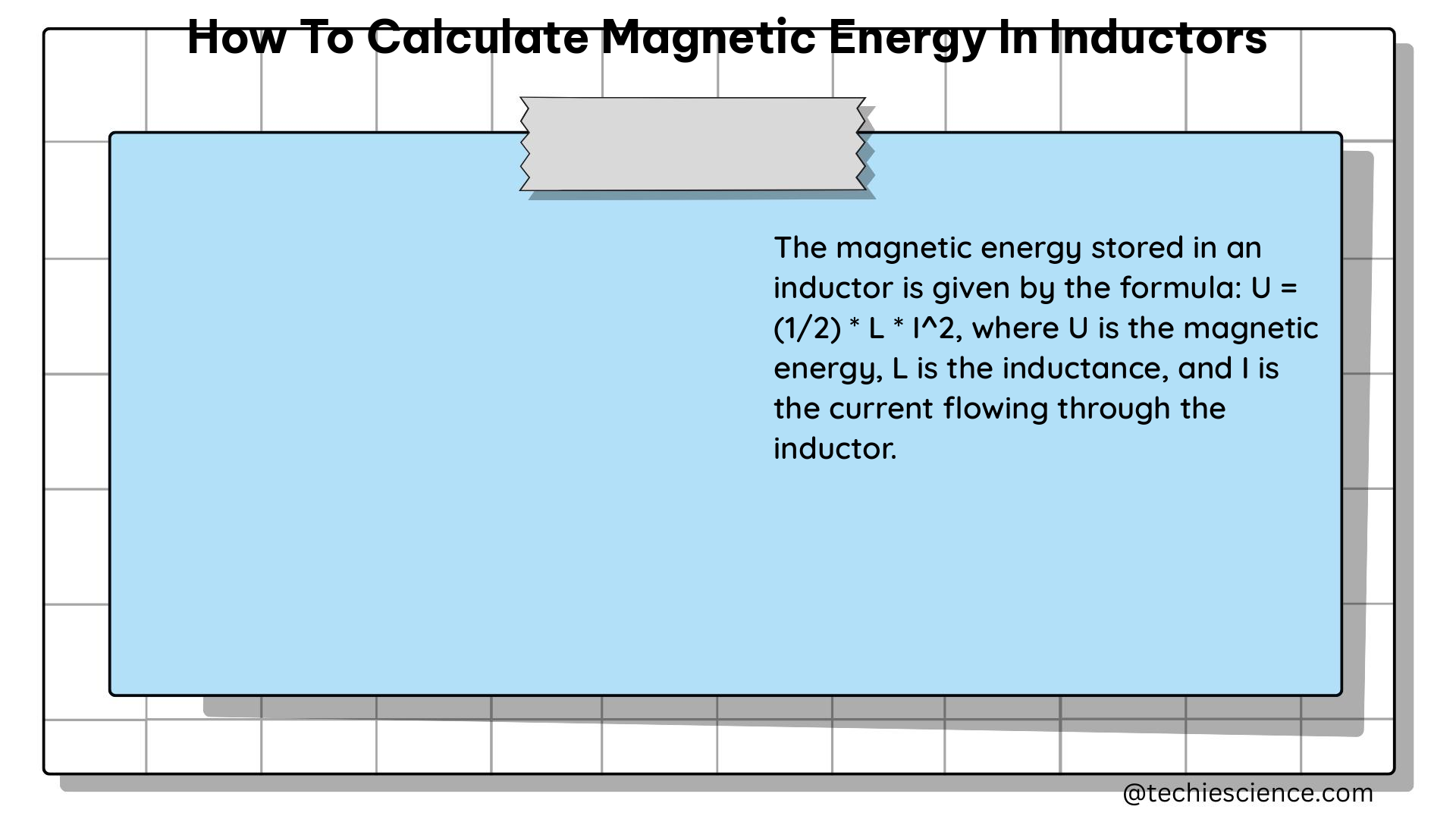
Inductors are passive electronic components that store energy in the form of a magnetic field. When current flows through an inductor, it creates a magnetic field, and this magnetic field stores energy. The amount of energy stored in the magnetic field is directly proportional to the inductance of the inductor and the square of the current flowing through it.
The formula for calculating the magnetic energy stored in an inductor is:
U = 1/2 * L * I^2
Where:
– U is the magnetic energy stored in the inductor (in joules)
– L is the inductance of the inductor (in henries)
– I is the current flowing through the inductor (in amperes)
This formula is derived from the principle of conservation of energy, which states that the energy stored in the magnetic field must be equal to the work done by the current source in establishing the magnetic field.
Calculating Magnetic Energy Density
In addition to the total magnetic energy stored in an inductor, it is also important to understand the concept of magnetic energy density. Magnetic energy density is the amount of energy stored per unit volume of the magnetic field.
The formula for calculating the magnetic energy density is:
u = 1/2 * μ0 * B^2
Where:
– u is the magnetic energy density (in joules per cubic meter)
– μ0 is the permeability of free space (4π × 10^-7 henries per meter)
– B is the magnetic field strength (in teslas)
This formula is derived from the relationship between the magnetic field strength, the magnetic flux density, and the permeability of the medium.
Practical Examples and Numerical Problems
Let’s consider a few practical examples to illustrate the application of these formulas.
Example 1:
Suppose we have an inductor with an inductance of 200 millihenries (mH) and a current of 15 amperes (A) flowing through it. Calculate the magnetic energy stored in the inductor.
Given:
– Inductance, L = 200 mH = 0.2 H
– Current, I = 15 A
Substituting the values in the formula:
U = 1/2 * L * I^2
U = 1/2 * 0.2 H * (15 A)^2
U = 22.5 J
Therefore, the magnetic energy stored in the inductor is 22.5 joules.
Example 2:
Suppose we have a magnetic field with a strength of 4.5 tesla (T). Calculate the magnetic energy density of the field.
Given:
– Magnetic field strength, B = 4.5 T
– Permeability of free space, μ0 = 4π × 10^-7 H/m
Substituting the values in the formula:
u = 1/2 * μ0 * B^2
u = 1/2 * (4π × 10^-7 H/m) * (4.5 T)^2
u = 9.4 × 10^6 J/m^3
Therefore, the magnetic energy density of the 4.5 tesla magnetic field is 9.4 × 10^6 joules per cubic meter.
Example 3:
An inductor has a cross-sectional area of 1 square centimeter (cm^2) and a length of 10 centimeters (cm). If the magnetic field strength inside the inductor is 0.5 tesla (T), calculate the total magnetic energy stored in the inductor.
Given:
– Cross-sectional area, A = 1 cm^2 = 1 × 10^-4 m^2
– Length, l = 10 cm = 0.1 m
– Magnetic field strength, B = 0.5 T
– Permeability of free space, μ0 = 4π × 10^-7 H/m
Step 1: Calculate the volume of the inductor.
Volume, `V = A * l = 1 × 10^-4 m^2 * 0.1 m = 1 × 10^-5 m^3`
Step 2: Calculate the magnetic energy density.
Magnetic energy density, `u = 1/2 * μ0 * B^2 = 1/2 * (4π × 10^-7 H/m) * (0.5 T)^2 = 9.9 × 10^-5 J/m^3`
Step 3: Calculate the total magnetic energy stored in the inductor.
Total magnetic energy, `U = u * V = 9.9 × 10^-5 J/m^3 * 1 × 10^-5 m^3 = 9.9 × 10^-10 J`
Therefore, the total magnetic energy stored in the inductor is 9.9 × 10^-10 joules.
Comparison with Capacitor Energy Storage
It’s important to note that the energy stored in an inductor is not in the form of potential energy, as it is in a capacitor, but rather in the form of kinetic energy of the electrons flowing through the inductor.
In a capacitor, the energy is stored in the form of an electric field between the plates, and the energy is proportional to the square of the voltage across the capacitor. In an inductor, the energy is stored in the form of a magnetic field, and the energy is proportional to the square of the current flowing through the inductor.
This difference in the form of energy storage has important implications for the behavior of inductors and capacitors in electrical circuits.
Conclusion
Calculating the magnetic energy stored in an inductor is a fundamental skill in electrical engineering and physics. By understanding the underlying principles, formulas, and practical examples, you can confidently tackle problems related to magnetic energy storage in inductors.
Remember to pay close attention to units, perform meticulous calculations, and consider the differences between the energy storage mechanisms in inductors and capacitors. With this comprehensive guide, you’ll be well on your way to mastering the calculation of magnetic energy in inductors.
References:
- Energy in a Magnetic Field – Physics – StudySmarter
- Energy Stored In an Inductor – Magnetic Field Energy Density
- How does an inductor store magnetic energy? – Physics Stack Exchange
- Energy Stored in Inductor: Theory & Examples | StudySmarter

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.