Calculating Magnetic Energy in MRI for Improved Imaging

Magnetic Resonance Imaging (MRI) is a powerful diagnostic tool that relies on the interaction between a strong magnetic field and the magnetic properties of the human body. To optimize the image quality and enhance the diagnostic capabilities of an MRI system, understanding the magnetic energy involved is crucial. In this comprehensive guide, we will delve into the key parameters and equations necessary to calculate the magnetic energy in an MRI setup, ultimately leading to improved imaging.

Magnetic Field Strength and Larmor Frequency

The foundation of MRI lies in the interaction between the magnetic field and the magnetic moments of the hydrogen protons within the human body. The strength of the magnetic field, denoted as B, is a crucial parameter that directly affects the magnetic energy and the Larmor frequency.

1. Magnetic Field Strength (B):
2. Measured in units of Tesla (T).
3. Typical MRI machines use magnetic fields ranging from 0.5 T to 3.0 T.

4. For example, a 1.0 T magnet has a magnetic field approximately 20,000 times stronger than the Earth’s magnetic field.

5. Larmor Frequency (f):

6. Calculated using the equation: f = γB, where γ is the Larmor constant (42.58 million cycles per Tesla for protons).
7. For a 1.0 T magnetic field, the Larmor frequency is approximately 42.58 million cycles per second.

The Larmor frequency represents the frequency at which the protons in the body precess around the applied magnetic field. This frequency is crucial for spatial encoding and signal detection in the MRI system.

Relaxation Times (T1 and T2)

The relaxation times, T1 and T2, are essential parameters that describe the behavior of the magnetization within the body during the MRI process.

1. Longitudinal Relaxation Time (T1):
2. Measures the time it takes for the magnetization to recover to its equilibrium state.
3. Calculated using the equation: Mz = M0(1 – e^(-t/T1)), where Mz is the longitudinal magnetization, M0 is the equilibrium magnetization, and t is the time.

4. Typical T1 values for human body tissues range from 0.1 to 4.0 seconds.

5. Transverse Relaxation Time (T2):

6. Measures the time it takes for the magnetization to decay in the transverse plane.
7. Calculated using the equation: Mxy = M0e^(-t/T2), where Mxy is the transverse magnetization.

The relaxation times directly impact the signal strength and contrast in the MRI image, making them crucial parameters to consider when optimizing the imaging process.

Magnetic Energy and Signal Strength

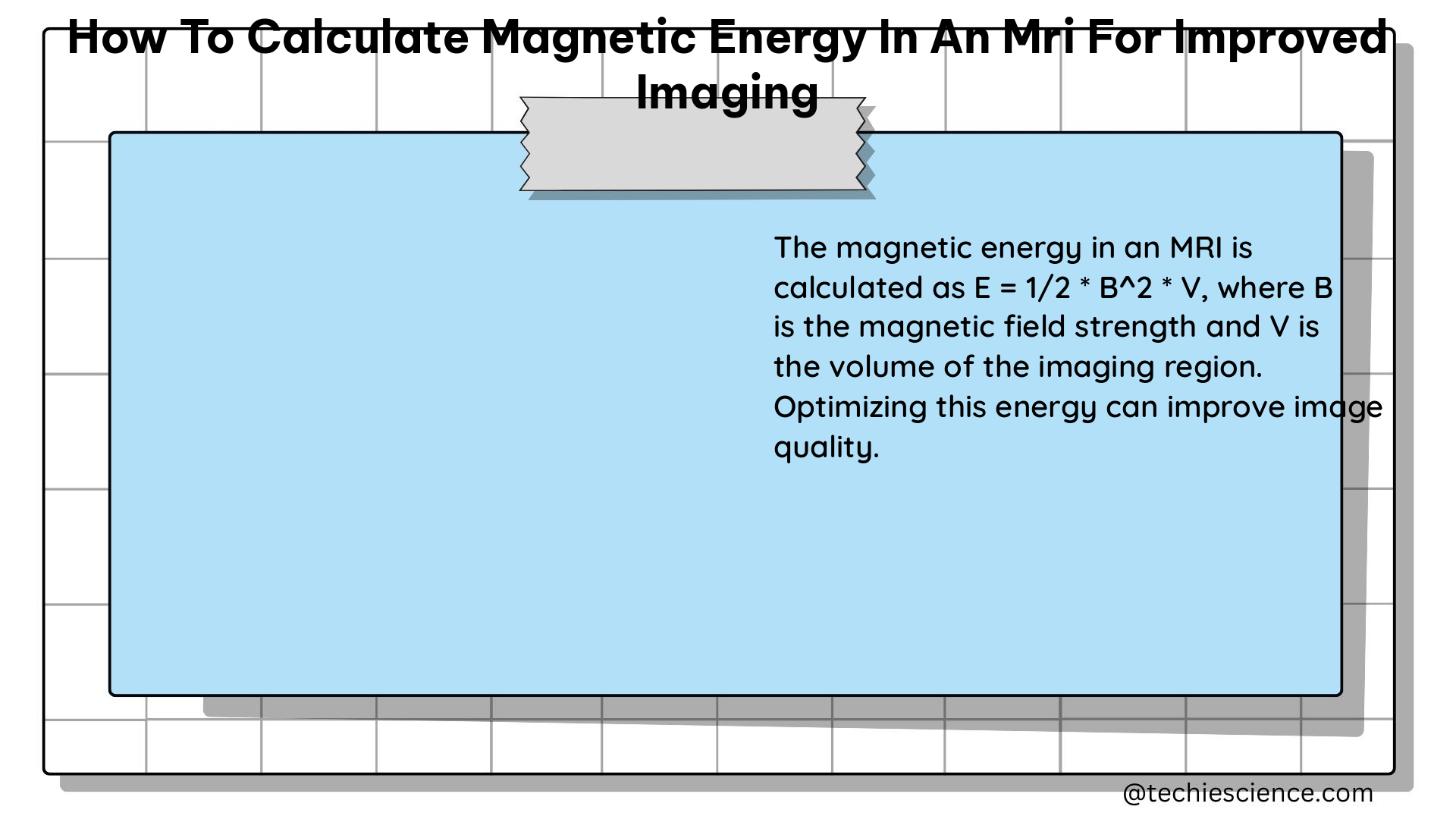
The magnetic energy associated with the MRI system is directly related to the strength of the magnetic field and the magnetization of the protons within the body.

1. Magnetic Energy (E):
2. The energy associated with the magnetic field and the magnetization of the protons.
3. Can be calculated using the equation: E = μB, where μ is the magnetic moment of the protons.

4. The magnetic moment, μ, is a vector quantity that represents the strength and direction of the magnetic field generated by the protons.

5. Signal Strength (S):

6. The strength of the MRI signal is directly proportional to the magnetic energy.
7. Can be calculated using the equation: S = k * M0 * B, where k is a constant and M0 is the equilibrium magnetization.

By optimizing the magnetic field strength and understanding the relationship between magnetic energy and signal strength, you can enhance the overall image quality and diagnostic capabilities of the MRI system.

Gradient Fields and Spatial Encoding

Gradient fields play a crucial role in the spatial encoding of the MRI signal, allowing for the reconstruction of the final image.

1. Gradient Fields:
2. Applied in the x, y, and z directions to create a unique magnetic field strength at each location within the body.

3. These gradient fields are used to spatially encode the MRI signal.

4. Spatial Encoding:

5. The process of assigning a unique frequency to each location based on the gradient fields.
6. This allows for the reconstruction of the MRI image by correlating the frequency information with the spatial location.

By carefully designing and controlling the gradient fields, you can optimize the spatial encoding process, leading to improved image resolution and clarity.

Fourier Transform and Image Reconstruction

The raw MRI signal data is transformed using the Fourier transform to convert it into a spatial image that can be interpreted by medical professionals.

1. Fourier Transform:
2. Used to convert the raw MRI signal into a spatial image.

3. The Fourier transform splits the signal into its constituent frequencies, which are then translated into spatial information.

4. Image Reconstruction:

5. The process of reconstructing the MRI image from the raw signal data.
6. Involves applying the Fourier transform and using the spatial encoding information to create a detailed image of the body.

Optimizing the Fourier transform and the image reconstruction algorithms can significantly enhance the quality and diagnostic value of the MRI images.

K-Space and Data Acquisition

The raw MRI signal data, known as k-space, contains the spatial frequency information that is essential for image reconstruction.

1. K-Space:
2. The raw MRI signal data before the Fourier transform.

3. Represents the spatial frequency information of the image.

4. Data Acquisition:

5. The process of collecting the raw MRI signal data.
6. Involves applying the gradient fields and measuring the signal strength at each location within the body.

Efficient data acquisition and effective k-space sampling strategies can contribute to improved image quality and reduced acquisition time, ultimately enhancing the overall MRI experience for both patients and medical professionals.

Conclusion

In conclusion, calculating the magnetic energy in an MRI system is a crucial step in optimizing the imaging process and improving the diagnostic capabilities of the technology. By understanding the relationships between magnetic field strength, Larmor frequency, relaxation times, gradient fields, Fourier transform, and data acquisition, you can fine-tune the MRI system to capture high-quality images that provide valuable insights for medical diagnosis and treatment.

References

1. Weishaupt, D., Köchli, V. D., & Marincek, B. (2008). How does MRI work?: An introduction to the physics and function of magnetic resonance imaging. Springer Science & Business Media.
2. Haacke, E. M., Brown, R. W., Thompson, M. R., & Venkatesan, R. (1999). Magnetic resonance imaging: physical principles and sequence design. Wiley-Liss.
3. Bernstein, M. A., King, K. F., & Zhou, X. J. (2004). Handbook of MRI pulse sequences. Elsevier.
4. Liang, Z. P., & Lauterbur, P. C. (2000). Principles of magnetic resonance imaging: a signal processing perspective. SPIE Optical Engineering Press.
5. Hornak, J. P. (1996). The basics of MRI. Henietta, NY: Interactive Learning Software.