How to Calculate the Force of Gravity: A Comprehensive Guide

The force of gravity is a fundamental concept in physics that describes the attractive force between two objects with mass. To calculate the force of gravity, we can use a simple formula that takes into account the masses of the objects and the distance between them. In this comprehensive guide, we will dive deep into the details of calculating the force of gravity, providing you with a thorough understanding of the underlying principles and practical applications.

Understanding the Gravitational Force Formula

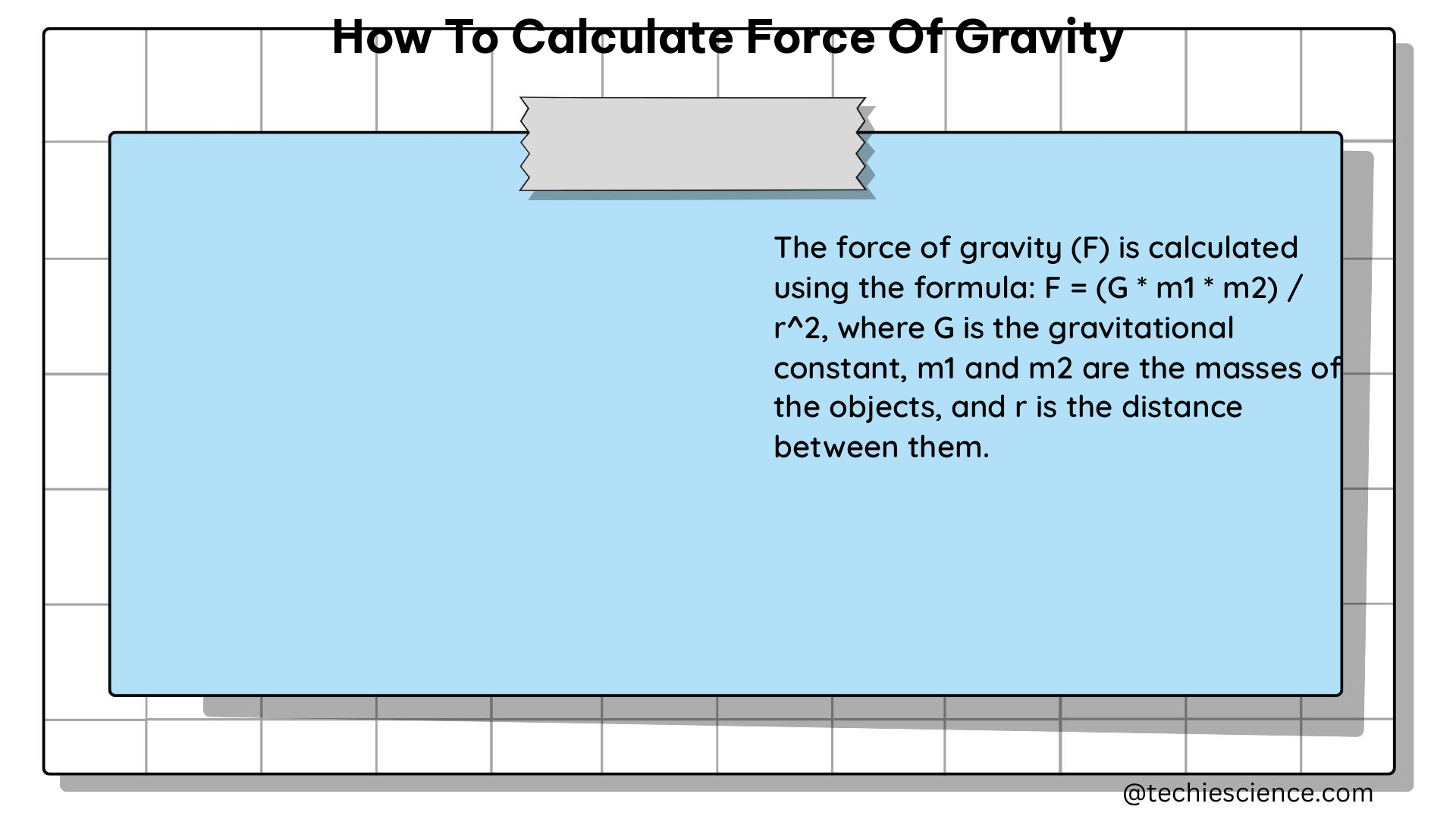
The formula used to calculate the force of gravity is known as Newton’s Law of Universal Gravitation. It states that the force of gravity between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The formula is expressed as:

F = (G * m1 * m2) / d^2

Where:
– F is the force of gravity (in Newtons, N)
– G is the gravitational constant (approximately 6.674 × 10^-11 N⋅m^2/kg^2)
– m1 and m2 are the masses of the two objects (in kilograms, kg)
– d is the distance between the centers of the two objects (in meters, m)

Let’s break down the components of this formula:

Gravitational Constant (G)

The gravitational constant, G, is a fundamental physical constant that represents the strength of the gravitational force between two objects. It is a universal constant, meaning it has the same value regardless of the location or the masses of the objects involved.

The value of the gravitational constant, G, is approximately 6.674 × 10^-11 N⋅m^2/kg^2. This value has been determined through extensive experimental measurements and is widely accepted in the scientific community.

Masses (m1 and m2)

The masses of the two objects, m1 and m2, are crucial factors in determining the force of gravity between them. The mass of an object is a measure of the amount of matter it contains and is typically expressed in kilograms (kg).

It’s important to note that the masses used in the formula should be the actual masses of the objects, not their weights. Weight is the force exerted on an object due to gravity, while mass is a measure of the amount of matter in the object, which remains constant regardless of the gravitational field.

Distance (d)

The distance, d, between the centers of the two objects is the final component in the gravitational force formula. This distance is typically measured in meters (m) and represents the separation between the objects.

It’s important to note that the distance used in the formula is the distance between the centers of the objects, not the distance between their surfaces. This is because the gravitational force is considered to act between the centers of the objects.

Calculating the Force of Gravity: Examples and Numerical Problems

Now that we have a solid understanding of the gravitational force formula, let’s apply it to some practical examples and numerical problems.

Example 1: Calculating the Force of Gravity between Two Masses

Suppose we have two objects with masses of 5 kg and 10 kg, respectively, and they are separated by a distance of 2 meters. Let’s calculate the force of gravity between these two objects.

Using the formula:
F = (G * m1 * m2) / d^2
F = (6.674 × 10^-11 N⋅m^2/kg^2 * 5 kg * 10 kg) / (2 m)^2
F = 8.3375 × 10^-9 N

Therefore, the force of gravity between the two objects is 8.3375 × 10^-9 Newtons.

Example 2: Calculating the Force of Gravity on the Earth’s Surface

The Earth’s mass is approximately 5.972 × 10^24 kg, and its radius is approximately 6,371 km. Let’s calculate the force of gravity on the surface of the Earth.

Using the formula:
F = (G * m1 * m2) / d^2
F = (6.674 × 10^-11 N⋅m^2/kg^2 * 5.972 × 10^24 kg * 1 kg) / (6.371 × 10^6 m)^2
F = 9.8 N

The force of gravity on the Earth’s surface is approximately 9.8 Newtons, which is the value commonly known as the acceleration due to gravity, or “g”.

Numerical Problem 1: Calculating the Force of Gravity between the Earth and the Moon

The mass of the Earth is approximately 5.972 × 10^24 kg, and the mass of the Moon is approximately 7.342 × 10^22 kg. The distance between the centers of the Earth and the Moon is approximately 3.84 × 10^8 m. Calculate the force of gravity between the Earth and the Moon.

Solution:
F = (G * m1 * m2) / d^2
F = (6.674 × 10^-11 N⋅m^2/kg^2 * 5.972 × 10^24 kg * 7.342 × 10^22 kg) / (3.84 × 10^8 m)^2
F = 1.98 × 10^20 N

Therefore, the force of gravity between the Earth and the Moon is approximately 1.98 × 10^20 Newtons.

Numerical Problem 2: Calculating the Force of Gravity between Two Satellites

Two satellites, each with a mass of 500 kg, are orbiting the Earth at an altitude of 500 km above the Earth’s surface. Calculate the force of gravity between the two satellites.

Given:
– Mass of each satellite (m1 = m2) = 500 kg
– Distance between the satellites (d) = 500 km + 6,371 km (Earth’s radius) = 6,871 m

Solution:
F = (G * m1 * m2) / d^2
F = (6.674 × 10^-11 N⋅m^2/kg^2 * 500 kg * 500 kg) / (6,871 m)^2
F = 1.12 × 10^-7 N

Therefore, the force of gravity between the two satellites is approximately 1.12 × 10^-7 Newtons.

Factors Affecting the Force of Gravity

The force of gravity can be influenced by several factors, including:

1. Mass: The masses of the objects involved directly affect the gravitational force. Larger masses result in a stronger gravitational force.

2. Distance: The distance between the objects is a crucial factor. As the distance increases, the gravitational force decreases rapidly, following the inverse square law.

3. Location: The gravitational force can vary depending on the location, as the Earth’s surface is not perfectly spherical, and the density of the underlying geological structures can affect the local gravitational field.

4. Altitude: The force of gravity decreases with increasing altitude, as the distance from the Earth’s center increases.

5. Rotation: The Earth’s rotation can also slightly affect the gravitational force, as it creates a centrifugal force that counteracts the gravitational force.

Understanding these factors is essential when calculating the force of gravity in different scenarios and applications.

Practical Applications of Calculating the Force of Gravity

The ability to calculate the force of gravity has numerous practical applications in various fields, including:

1. Astronomy and Astrophysics: Calculating the gravitational force between celestial bodies, such as planets, stars, and galaxies, is crucial for understanding the dynamics of the universe and predicting the motion of these objects.

2. Satellite Orbits: Calculating the gravitational force between satellites and the Earth is essential for designing and maintaining stable satellite orbits, ensuring accurate positioning and communication.

3. Geophysics: Measuring variations in the Earth’s gravitational field can provide insights into the planet’s internal structure, density, and composition, which is valuable for geological and geophysical studies.

4. Engineering: Understanding the gravitational force is crucial in the design of structures, such as buildings, bridges, and dams, to ensure they can withstand the forces acting upon them.

5. Ballistics and Projectile Motion: Calculating the gravitational force is essential in predicting the trajectory of projectiles, such as in the design of weapons or the analysis of sports like archery and golf.

6. Gravitational Waves: The detection and analysis of gravitational waves, predicted by Einstein’s theory of general relativity, rely on the accurate calculation of gravitational forces between massive objects.

By mastering the techniques for calculating the force of gravity, you can unlock a deeper understanding of the physical world and contribute to advancements in various scientific and technological fields.

Conclusion

In this comprehensive guide, we have explored the fundamental principles and practical applications of calculating the force of gravity. By understanding the gravitational force formula, the role of the gravitational constant, and the factors that influence the gravitational force, you now have the tools to tackle a wide range of problems and scenarios involving the force of gravity.

Remember, the ability to accurately calculate the force of gravity is not just a theoretical exercise but a crucial skill that has real-world implications in fields ranging from astronomy and engineering to geophysics and ballistics. As you continue your journey in physics, keep exploring and applying these concepts to deepen your understanding and contribute to the advancement of scientific knowledge.

Reference:

1. Isaac Newton’s Formula for the Force of Gravity: Definition & Example
2. The Value of g
3. How to Calculate Force of a Fall w/ Increased Gravity
4. Gravitational Constant
5. Earth’s Mass and Radius
6. Moon’s Mass
7. Satellite Altitude