How to Calculate Energy Transport in Thermal Conduction

Thermal conduction is a fundamental mode of heat transfer, where energy is transported through the vibration of atoms and molecules within a material without the involvement of any bulk motion of the material. To calculate the energy transport in thermal conduction, we can use the formula for heat transfer through conduction, which is given by:

Q/t = kA(T1 - T2)/d

where Q/t is the rate of heat transfer, k is the thermal conductivity of the material, A is the cross-sectional area, T1 and T2 are the temperatures at the two ends of the material, and d is the thickness of the material.

Understanding Thermal Conductivity

The thermal conductivity (k) is a measure of a material’s ability to conduct heat. It is measured in watts per meter-kelvin (W/mK). Table 1 below provides representative values of thermal conductivity for various materials:

Material	Thermal Conductivity (W/mK)
Silver	429
Copper	401
Aluminum	237
Iron	80.2
Glass	1.05
Brick	0.69
Wood (oak)	0.17
Glass Wool	0.04
Styrofoam	0.03

The higher the thermal conductivity of a material, the better it is at conducting heat. Materials with low thermal conductivity, such as glass wool and Styrofoam, are often used as insulation to reduce heat transfer.

Calculating Heat Transfer through Conduction

Let’s consider an example to calculate the rate of heat conduction through a house wall.

Suppose the house wall is 13.0 cm thick and has an average thermal conductivity twice that of glass wool. The surface area of the walls is 120 m^2, and the inside surface is at 18.0°C, while the outside surface is at 5.00°C.

Using the formula for heat transfer through conduction, we can calculate the rate of heat conduction as follows:

Q/t = kA(T1 - T2)/d
= (2 * k_glass wool) * A * (18.0°C - 5.00°C) / 0.13 m

where k_glass wool is the thermal conductivity of glass wool, which is approximately 0.04 W/mK.

To find the value of A, we can use the surface area of the walls, which is 120 m^2.

Therefore, the rate of heat conduction is:

Q/t = (2 * 0.04 W/mK) * 120 m^2 * (18.0°C - 5.00°C) / 0.13 m
= 9737.7 W or 9.74 kW

This means that 9.74 kilowatts of heat are being conducted through the house walls per second.

Other Concepts and Formulas

In addition to the formula for heat transfer through conduction, there are other related concepts and formulas that are important for understanding energy transport in thermal conduction:

Heat Flux

Heat flux is the rate of heat transfer per unit area, expressed in watts per square meter (W/m^2). It can be calculated using the formula:

q = Q/A

where q is the heat flux, Q is the rate of heat transfer, and A is the cross-sectional area.

Thermal Conductivity of Composite Materials

When dealing with composite materials, the rate of heat transfer through the system can be expressed as the sum of the rates of heat transfer through each individual material, divided by the total thickness of the system. This is known as the thermal conductivity of composite materials.

Heat Transfer in Cylinders and Spheres

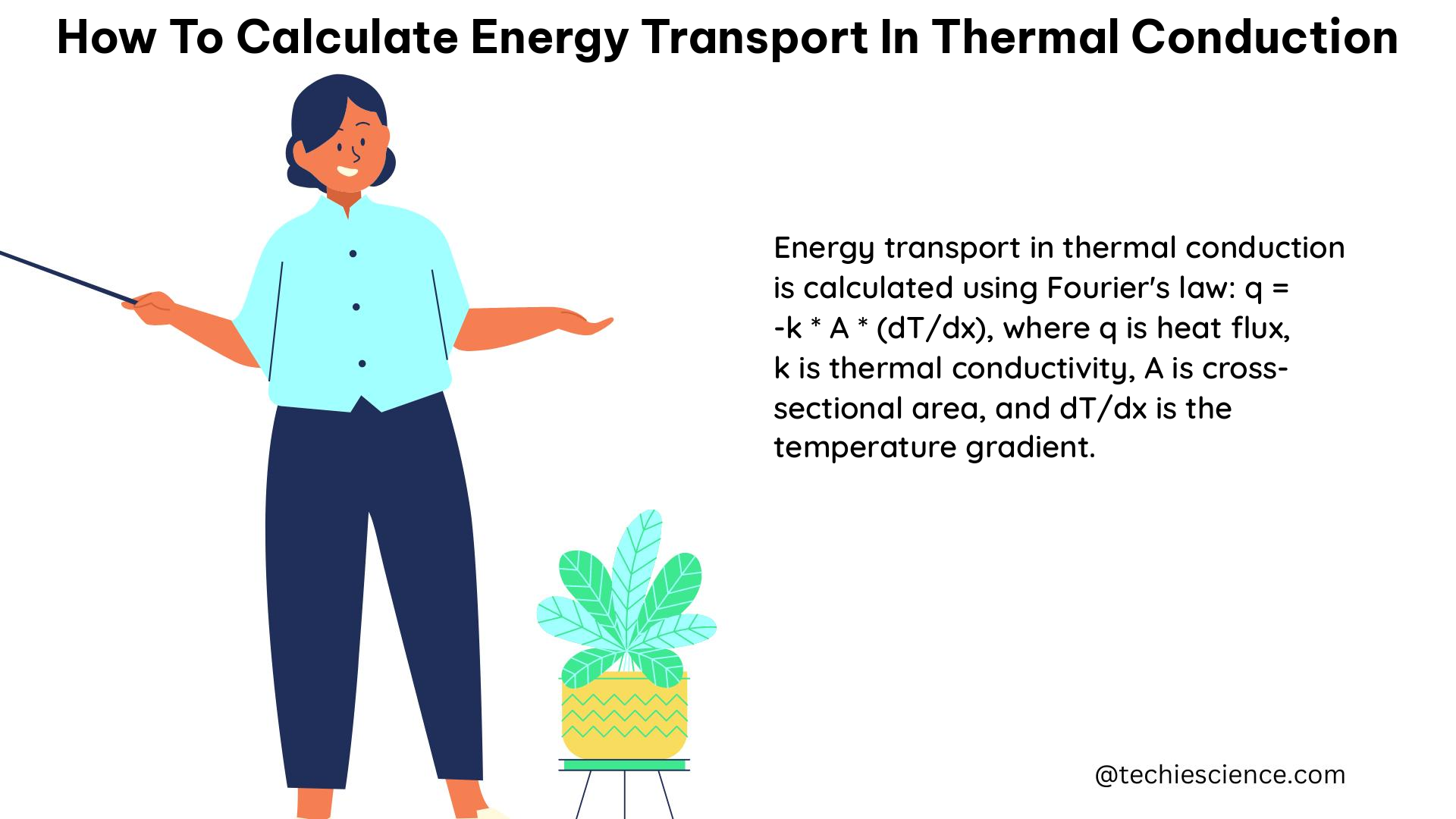
The rate of heat transfer through a cylinder or sphere can be calculated using the Fourier law of heat conduction, which states that the rate of heat transfer is proportional to the temperature gradient (dT/dx) and the thermal conductivity of the material.

Numerical Examples

1. Heat Conduction through a Copper Plate
2. Copper plate dimensions: 20 cm × 30 cm × 2 cm
3. Temperature difference across the plate: 50°C
4. Thermal conductivity of copper: 401 W/mK
5. Calculate the rate of heat conduction through the plate.

Solution:
Q/t = kA(T1 - T2)/d
= 401 W/mK * (0.2 m * 0.3 m) * (50°C) / 0.02 m
= 3009 W

1. Heat Conduction through a Composite Wall
2. Wall composition: 2 cm of brick, 5 cm of glass wool, and 3 cm of wood
3. Temperature difference across the wall: 20°C
4. Thermal conductivities: brick (0.69 W/mK), glass wool (0.04 W/mK), wood (0.17 W/mK)
5. Calculate the rate of heat conduction through the composite wall.

Solution:
Q/t = (k_brick * A_brick / d_brick) + (k_glass_wool * A_glass_wool / d_glass_wool) + (k_wood * A_wood / d_wood)
= (0.69 W/mK * 1 m^2 / 0.02 m) + (0.04 W/mK * 1 m^2 / 0.05 m) + (0.17 W/mK * 1 m^2 / 0.03 m)
= 34.5 W + 0.8 W + 5.67 W
= 40.97 W

These examples demonstrate how to apply the formula for heat transfer through conduction to calculate the rate of energy transport in different scenarios.

Conclusion

In this blog post, we have explored the fundamental concepts and formulas for calculating energy transport in thermal conduction. We have discussed the importance of thermal conductivity, the formula for heat transfer through conduction, and other related concepts such as heat flux and thermal conductivity of composite materials. Additionally, we have provided numerical examples to illustrate the application of these principles.

Understanding the principles of thermal conduction and the ability to calculate energy transport is crucial in various fields, including engineering, architecture, and materials science. By mastering these concepts, you can optimize the design and performance of systems that involve heat transfer, leading to improved energy efficiency, thermal management, and overall system performance.

References

1. Conduction | Physics – Lumen Learning: https://courses.lumenlearning.com/suny-physics/chapter/14-5-conduction/
2. Steady Conduction Heat Transfer.pdf: https://www.sfu.ca/~mbahrami/ENSC%20388/Notes/Steady%20Conduction%20Heat%20Transfer.pdf
3. Heat Transfer Through Conduction Equation & Examples – Study.com: https://study.com/academy/lesson/heat-transfer-through-conduction-equation-examples.html
4. Chapter 13 Soil Heat Flow. | Calculus-Integration – Bookdown: https://bookdown.org/huckley/Physical_Processes_In_Ecosystems/soilheatflow.html