Calculating energy in quantum computing is a crucial aspect of understanding the behavior and properties of quantum systems. This comprehensive guide will delve into the various methods and formulas used to determine energy in the realm of quantum computing, providing you with a detailed and technical understanding of this topic.
Quantum Monte Carlo Method for Ground State Energy Calculation
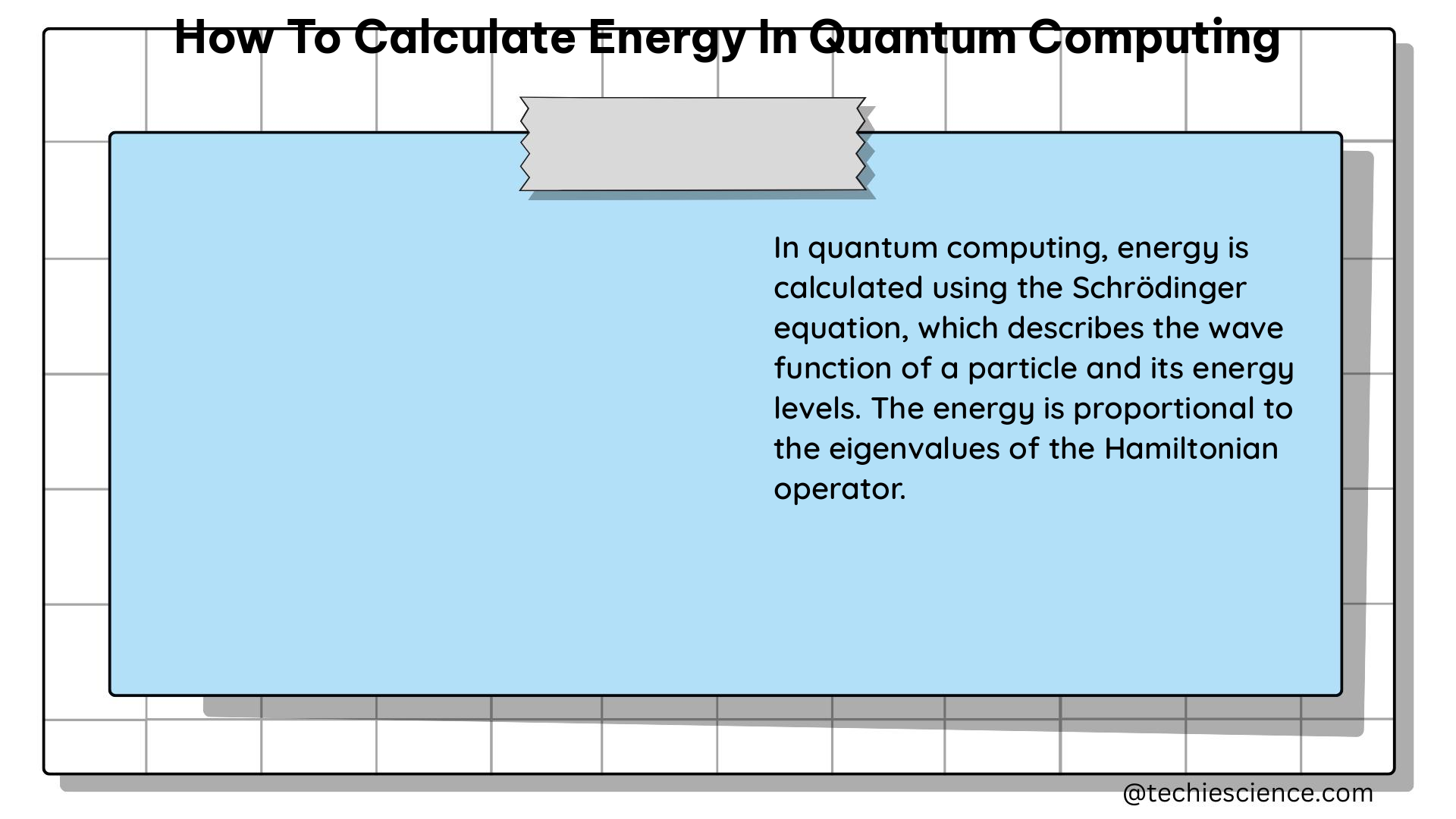
The Quantum Monte Carlo (QMC) method is a powerful tool for calculating the ground state energy of molecules in quantum computing. This method involves solving the Schrödinger equation, which describes the behavior of quantum systems, to determine the lowest energy state of a molecule.
The Schrödinger equation is given by:
Hψ = Eψ
where H is the Hamiltonian operator, ψ is the wavefunction, and E is the energy eigenvalue.
The ground state energy, which is the lowest energy state of a molecule, is encoded in the solution to this equation. However, as the size of the molecule increases, the complexity of solving the Schrödinger equation grows exponentially, making it challenging to solve on classical computers.
Quantum computers, on the other hand, can handle these exponentially larger and more complex calculations due to the unique properties of qubits. Unlike classical bits, which can only exist in a state of 0 or 1, qubits can exist in a superposition of these states, allowing them to represent and process information in a more efficient manner.
In a study by Reichman and Lee with researchers at Google Quantum AI, they used an algorithm that reduces the statistical errors, or noise, produced by qubits in crunching chemistry equations. They used up to 16 qubits on Sycamore, Google’s 53-qubit computer, to calculate the ground state energy of three molecules: heliocide (H4), molecular nitrogen (N2), and solid diamond.
The results of this study demonstrate the potential of quantum computers to solve complex problems in quantum chemistry, such as determining the ground state energy of molecules, which is a crucial step in understanding their behavior and properties.
Potential Energy Surfaces (PESs) in Quantum Computing
Potential Energy Surfaces (PESs) are mathematical surfaces that describe the potential energy of a system of particles, such as atoms, as a function of their positions. These surfaces are widely used in quantum chemistry to study the behavior of molecules and predict their properties.
In quantum computing, chemically accurate PESs can be generated by measuring the density of the system, which is a measure of the probability of finding a particle in a particular region of space. By measuring the density at different points in space, a PES can be constructed.
The density of a quantum system is given by the square of the wavefunction, |ψ|^2, which represents the probability distribution of the particles in the system. This can be measured on a quantum computer by performing measurements on the qubits that represent the system.
Once the density is measured, the potential energy of the system can be calculated by integrating the density over the volume of the system. This process can be repeated for different configurations of the particles, allowing the construction of a complete PES.
The ability to generate accurate PESs on quantum computers is a significant advancement in the field of quantum chemistry, as it allows for the study of complex molecular systems and the prediction of their properties.
Energy Levels Estimation on a Quantum Computer
Another method for calculating energy in quantum computing is the estimation of energy levels of physical systems on a quantum computer. This method is based on the study of the evolution of a quantum system over time.
The energy levels of a quantum system are determined by the eigenvalues of the Hamiltonian operator, H, which describes the total energy of the system. By measuring the evolution of the system, the energy levels can be estimated.
The evolution of a quantum system is described by the time-dependent Schrödinger equation:
i ℏ ∂ψ/∂t = Hψ
where ℏ is the reduced Planck constant.
By measuring the evolution of the system, the energy levels can be estimated using techniques such as the Quantum Phase Estimation algorithm. This algorithm allows for the estimation of the eigenvalues of the Hamiltonian operator, which correspond to the energy levels of the system.
The ability to estimate energy levels on a quantum computer is crucial for the study of the behavior of molecules and the prediction of their properties. This information can be used to understand the chemical and physical processes that occur in these systems, and to design new materials and molecules with desired properties.
Quantum Energy of Light
The energy of a photon, which is the fundamental particle of light, can be calculated using the following formulas:
E = hfE = hc/λ
where:
– E is the energy of the photon in Joules (J)
– h is the Planck constant, which is approximately 6.63 × 10^-34 J⋅s
– f is the frequency of the photon in Hertz (Hz)
– c is the speed of light in a vacuum, which is approximately 3 × 10^8 m/s
– λ is the wavelength of the photon in meters (m)
These formulas can be used to calculate the quantum energy of light, which is composed of photons. For example, the quantum energy of a red laser in a vacuum with a frequency of 4.5 × 10^14 Hz is 2.98 × 10^-19 J, and the quantum energy of a blue laser in a vacuum with a wavelength of 4.8 × 10^-7 m is 4.14 × 10^-19 J.
Understanding the quantum energy of light is important in quantum computing, as photons can be used to transmit and process information in quantum systems. The ability to calculate the energy of photons can help in the design and optimization of quantum communication and information processing systems.
Conclusion
In this comprehensive guide, we have explored the various methods and formulas used to calculate energy in quantum computing. From the Quantum Monte Carlo method for ground state energy calculation to the estimation of energy levels on a quantum computer and the quantum energy of light, we have covered a wide range of techniques that are crucial for understanding the behavior and properties of quantum systems.
By mastering these concepts, you will be well-equipped to tackle complex problems in quantum chemistry, materials science, and other fields that rely on the accurate calculation of energy in quantum computing. Remember to continue exploring and experimenting with these methods to deepen your understanding and push the boundaries of what is possible in the exciting world of quantum computing.
References
- Toward a quantum computer that calculates molecular energy. (2022, March 16). Retrieved from https://phys.org/news/2022-03-quantum-molecular-energy.html
- Calculating Potential Energy Surfaces with Quantum Computers. (2024, April 11). Retrieved from https://pubs.acs.org/doi/10.1021/acs.jctc.3c01177
- Energy levels estimation on a quantum computer by evolution of a quantum system. (2022, February 6). Retrieved from https://www.sciencedirect.com/science/article/pii/S0375960121007076
- How to Calculate the Quantum Energy of Light | Physics – Study.com. (2021, December 1). Retrieved from https://study.com/skill/learn/how-to-calculate-the-quantum-energy-of-light-explanation.html

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.