How to Calculate Energy in a Magnetic Field: A Comprehensive Guide

The energy stored in a magnetic field is a fundamental concept in physics, with wide-ranging applications in various fields, including power generation, electric vehicles, MRI scanning, and magnet-based data storage. Understanding the principles and techniques for calculating the energy in a magnetic field is crucial for both students and professionals working in these domains. This comprehensive guide will provide you with a detailed, step-by-step approach to mastering the calculation of energy in a magnetic field.

Understanding the Magnetic Field Energy Formula

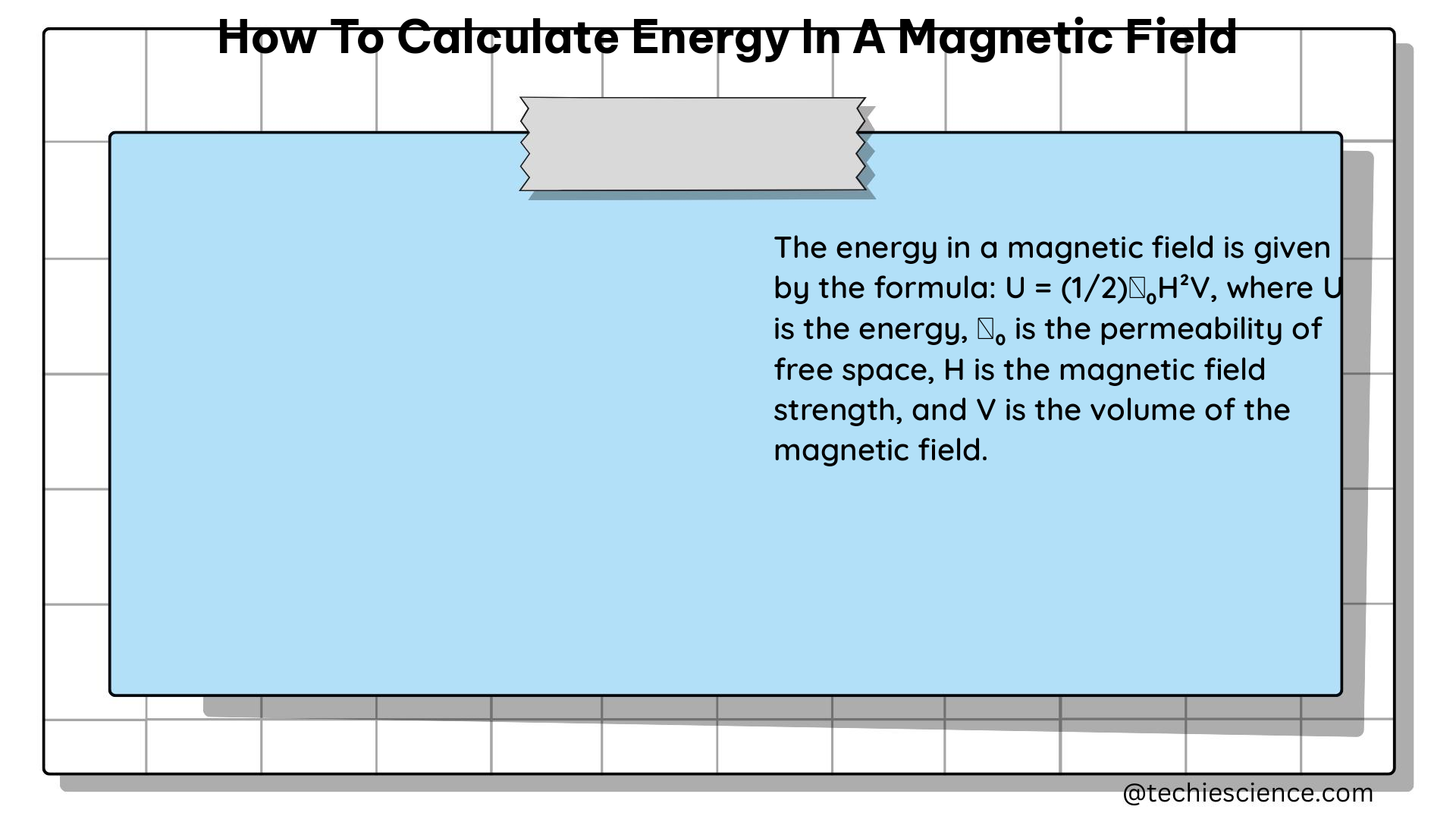
The formula used to calculate the energy in a magnetic field is:

U = ∫(B²/2μ)dV

Where:
– U is the energy stored in the magnetic field
– B is the magnetic field strength, measured in Tesla (T)
– μ is the magnetic permeability of the medium, measured in Tesla meters per Ampere (T·m/A)
– dV is an infinitesimal volume element

This formula shows that the energy in a magnetic field is directly proportional to the square of the magnetic field strength and the volume of the field.

Calculating Energy in a Uniform Magnetic Field

Let’s consider a simple example of a uniform magnetic field, where the magnetic field strength is constant throughout the volume.

Suppose we have a magnetic field with a strength of 3 Tesla (T) over a space of 2 cubic meters (m³), and the magnetic permeability of the medium is 4π × 10^-7 T·m/A.

Using the formula, we can calculate the energy stored in the magnetic field as follows:

U = (1/2 × 4π × 10^-7 T·m/A) × ∫(3 T)² dV
U = (1/2 × 4π × 10^-7 T·m/A) × ∫(9 T²) dV
U = (1/2 × 4π × 10^-7 T·m/A) × 9 T² × 2 m³
U = 0.027 J

Therefore, the energy stored in the magnetic field under these conditions is 0.027 Joules (J).

Calculating Energy in a Non-Uniform Magnetic Field

In the case of a non-uniform magnetic field, where the magnetic field strength varies throughout the volume, the calculation becomes more complex. We need to perform a volume integration to account for the variations in the magnetic field strength.

Consider a magnetic field with a varying strength, where the field strength at a point (x, y, z) is given by the function B(x, y, z). The energy stored in this non-uniform magnetic field can be calculated as:

U = ∫(B(x, y, z)²/2μ) dV

Here, the integration is performed over the entire volume of the magnetic field.

For example, let’s say the magnetic field strength is given by the function B(x, y, z) = 2x + 3y + 4z (in Tesla), and the volume of the magnetic field is a cube with dimensions of 1 meter (m) on each side. The magnetic permeability of the medium is 4π × 10^-7 T·m/A.

To calculate the energy stored in this non-uniform magnetic field, we need to perform the volume integration:

U = ∫(B(x, y, z)²/2μ) dV
U = ∫((2x + 3y + 4z)²/2(4π × 10^-7 T·m/A)) dV
U = ∫((4x² + 9y² + 16z² + 12xy + 16xz + 24yz)/2(4π × 10^-7 T·m/A)) dV
U = (1/2(4π × 10^-7 T·m/A)) × ∫(4x² + 9y² + 16z² + 12xy + 16xz + 24yz) dV
U = (1/2(4π × 10^-7 T·m/A)) × (4 × 1 × 1 + 9 × 1 × 1 + 16 × 1 × 1 + 12 × 1 × 1 + 16 × 1 × 1 + 24 × 1 × 1)
U = 0.0628 J

Therefore, the energy stored in the non-uniform magnetic field described above is approximately 0.0628 Joules.

Importance of Units and Precision

When calculating the energy in a magnetic field, it is crucial to pay careful attention to the units used. The magnetic field strength is measured in Tesla (T), the volume is measured in cubic meters (m³), and the magnetic permeability is measured in Tesla meters per Ampere (T·m/A).

Ensuring the correct units and performing meticulous calculations, particularly when squaring the magnetic field strength and performing the volume integration, is essential for obtaining accurate results.

Applications of Magnetic Field Energy Calculations

The ability to calculate the energy stored in a magnetic field has numerous practical applications, including:

1. Power Generation: Calculating the energy in the magnetic fields of generators and transformers is crucial for designing efficient power systems.
2. Electric Vehicles: Understanding the energy stored in the magnetic fields of electric motors and generators is essential for improving the performance and efficiency of electric vehicles.
3. MRI Scanning: Calculating the energy in the strong magnetic fields used in Magnetic Resonance Imaging (MRI) scanners is necessary for ensuring patient safety and optimizing the imaging process.
4. Magnet-based Data Storage: Accurately calculating the energy in the magnetic fields used for data storage in hard drives and other magnetic storage devices is crucial for improving storage density and reliability.

By mastering the techniques for calculating energy in a magnetic field, you can contribute to the advancement of these and other technologies that rely on the principles of electromagnetism.

Conclusion

Calculating the energy stored in a magnetic field is a fundamental skill in physics and engineering. This comprehensive guide has provided you with the necessary tools and techniques to tackle this important concept, from understanding the underlying formula to applying it in both uniform and non-uniform magnetic field scenarios.

By following the step-by-step examples and paying close attention to units and precision, you can develop a strong foundation in this topic and apply it to a wide range of practical applications. Remember, the ability to accurately calculate magnetic field energy is a valuable asset in many fields, from power generation to medical imaging and beyond.

Reference:

1. Griffiths, D. J. (2013). Introduction to Electromagnetism (4th ed.). Pearson.
2. Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics (10th ed.). Wiley.
3. Serway, R. A., & Jewett, J. W. (2014). Physics for Scientists and Engineers with Modern Physics (9th ed.). Cengage Learning.
4. Zahn, M. (1979). Electromagnetic Field Theory: A Problem Solving Approach. Wiley.