How to Calculate Energy in a Cyclotron Motion: A Comprehensive Guide

Calculating the energy in a cyclotron motion is a crucial aspect of understanding the behavior of charged particles in a magnetic field. In this comprehensive guide, we will delve into the fundamental principles, formulas, and examples to help you master the art of energy calculation in a cyclotron.

Understanding Cyclotron Motion

A cyclotron is a type of particle accelerator that uses a constant magnetic field and an oscillating electric field to accelerate charged particles, such as protons or ions, to high energies. The charged particles move in a circular path, known as the cyclotron motion, due to the combined effect of the magnetic and electric fields.

Kinetic Energy of Charged Particles in a Cyclotron

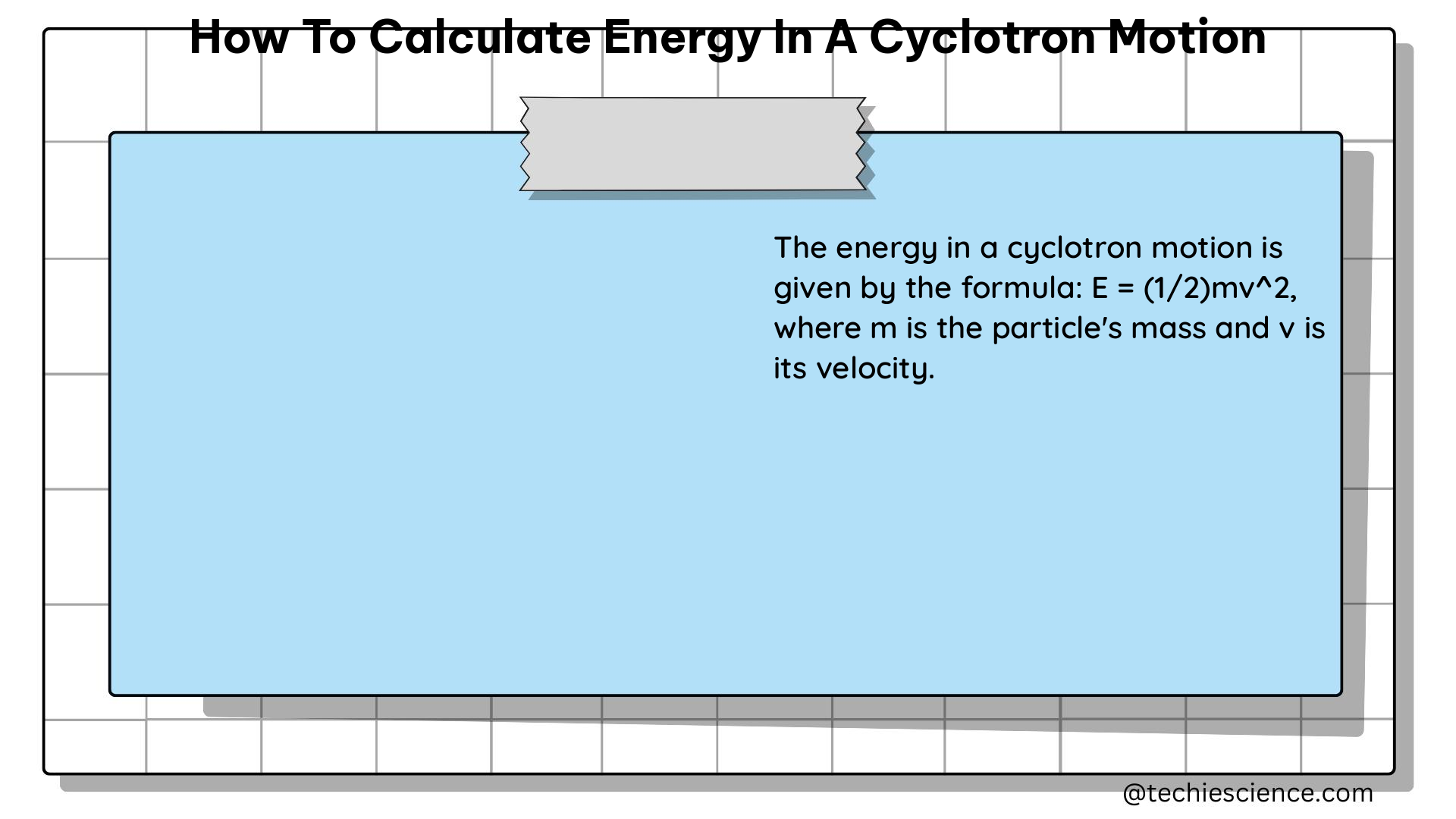
The kinetic energy of a charged particle in a cyclotron is given by the formula:

Ek = 1/2 * m * v^2

where:
– Ek is the kinetic energy of the particle
– m is the mass of the particle
– v is the velocity of the particle

As the particle moves through the cyclotron, its velocity increases with each turn, leading to an increase in its kinetic energy.

Energy Gained by Charged Particles in a Cyclotron

The energy gained by a charged particle with charge e accelerated by a voltage U in a cyclotron is given by the formula:

Ek = e * U

where:
– Ek is the kinetic energy of the particle
– e is the charge of the particle
– U is the voltage applied to the cyclotron

This formula allows us to calculate the energy gained by the particle as it is accelerated by the electric field in the cyclotron.

Calculating the Cyclotron Motion Radius

The radius of the circular path followed by a charged particle in a cyclotron is given by the formula:

r = m * v / (q * B)

where:
– r is the radius of the cyclotron motion
– m is the mass of the particle
– v is the velocity of the particle
– q is the charge of the particle
– B is the strength of the magnetic field

This formula allows us to determine the size of the cyclotron based on the properties of the charged particles and the magnetic field.

Calculating the Maximum Energy in a Cyclotron

The maximum energy that a particle can reach in a cyclotron is given by the formula:

Em = n * Ek

where:
– Em is the maximum energy of the particle
– n is the number of turns the particle makes in the cyclotron
– Ek is the kinetic energy of the particle

By knowing the number of turns and the energy gained per turn, we can calculate the maximum energy that the particle can achieve in the cyclotron.

Example Calculation

Let’s consider an example where we have a cyclotron with a magnetic field strength of 1 Tesla, and we want to accelerate protons (mass of 1.67 × 10^-27 kg and charge of 1.6 × 10^-19 C) to an energy of 10 MeV.

1. Calculate the voltage required:
   U = Ek / e = (1/2 * m * v^2) / e = (1/2 * 1.67 × 10^-27 kg * v^2) / (1.6 × 10^-19 C)
v = sqrt(2 * U * e / m) = sqrt(2 * 10 MeV * 1.6 × 10^-19 C / 1.67 × 10^-27 kg) = 2.1 × 10^7 m/s
U = (1/2 * 1.67 × 10^-27 kg * (2.1 × 10^7 m/s)^2) / (1.6 × 10^-19 C) = 50 kV

2. Calculate the radius of the cyclotron orbit:
   r = m * v / (q * B) = 1.67 × 10^-27 kg * 2.1 × 10^7 m/s / (1.6 × 10^-19 C * 1 T) = 0.21 m

3. Calculate the number of turns required to reach 10 MeV:
   n = Em / Ek = 10 MeV / (1/2 * m * v^2) = 10 MeV / (1/2 * 1.67 × 10^-27 kg * (2.1 × 10^7 m/s)^2) = 2.5 × 10^5 turns

Therefore, to accelerate protons to an energy of 10 MeV in this cyclotron, we need to apply a voltage of 50 kV and let the protons make 2.5 × 10^5 turns.

Additional Considerations

• The energy gained by the charged particles in a cyclotron is directly proportional to the voltage applied and the number of turns they make.
• The radius of the cyclotron motion is influenced by the mass, charge, and velocity of the particles, as well as the strength of the magnetic field.
• The maximum energy that can be achieved in a cyclotron is limited by the size of the cyclotron and the strength of the magnetic field.
• Cyclotrons are commonly used in various applications, such as medical imaging, cancer treatment, and scientific research.

Conclusion

Calculating the energy in a cyclotron motion is a fundamental skill for understanding the behavior of charged particles in particle accelerators. By mastering the formulas and principles presented in this guide, you can confidently determine the energy, velocity, and motion of charged particles in a cyclotron, enabling you to design and optimize these systems for various applications.

References

1. Cyclotron Basics and Calculations
2. How to Calculate the Energy Input Needed for a Cyclotron Reactor
3. Hanneke’s PhD Thesis on Cyclotron Design