Calculating Energy Dissipation in Turbulent Flows: A Comprehensive Guide

Turbulent flows are ubiquitous in various engineering applications, from aerodynamics to fluid machinery. Understanding the energy dissipation in these flows is crucial for optimizing system performance, predicting heat transfer, and analyzing the dynamics of multiphase systems. This comprehensive guide will delve into the fundamental concepts, mathematical formulations, and practical applications of calculating energy dissipation in turbulent flows.

Understanding Turbulent Kinetic Energy (TKE) and Its Dissipation Rate

Turbulent kinetic energy (TKE) is the kinetic energy associated with the fluctuating velocity components in a turbulent flow. It represents the energy contained in the turbulent eddies and is a crucial parameter in the analysis of turbulent flows. The TKE can be calculated as:

TKE = 1/2 * (u’^2 + v’^2 + w’^2)

where u’, v’, and w’ are the fluctuating velocity components in the x, y, and z directions, respectively.

The dissipation rate of TKE, denoted as ε, is the rate at which the TKE is converted into heat due to viscous forces. This dissipation rate is a fundamental quantity in turbulence modeling and is typically calculated using the following formula:

ε = Cμ * (TKE)^(3/2) / L

where:
– ε is the dissipation rate of TKE
– Cμ is a constant, typically around 0.09
– TKE is the turbulent kinetic energy
– L is the turbulent length scale, which represents the size of the largest energy-containing eddies in the flow

Estimating Turbulent Intensity and Length Scale

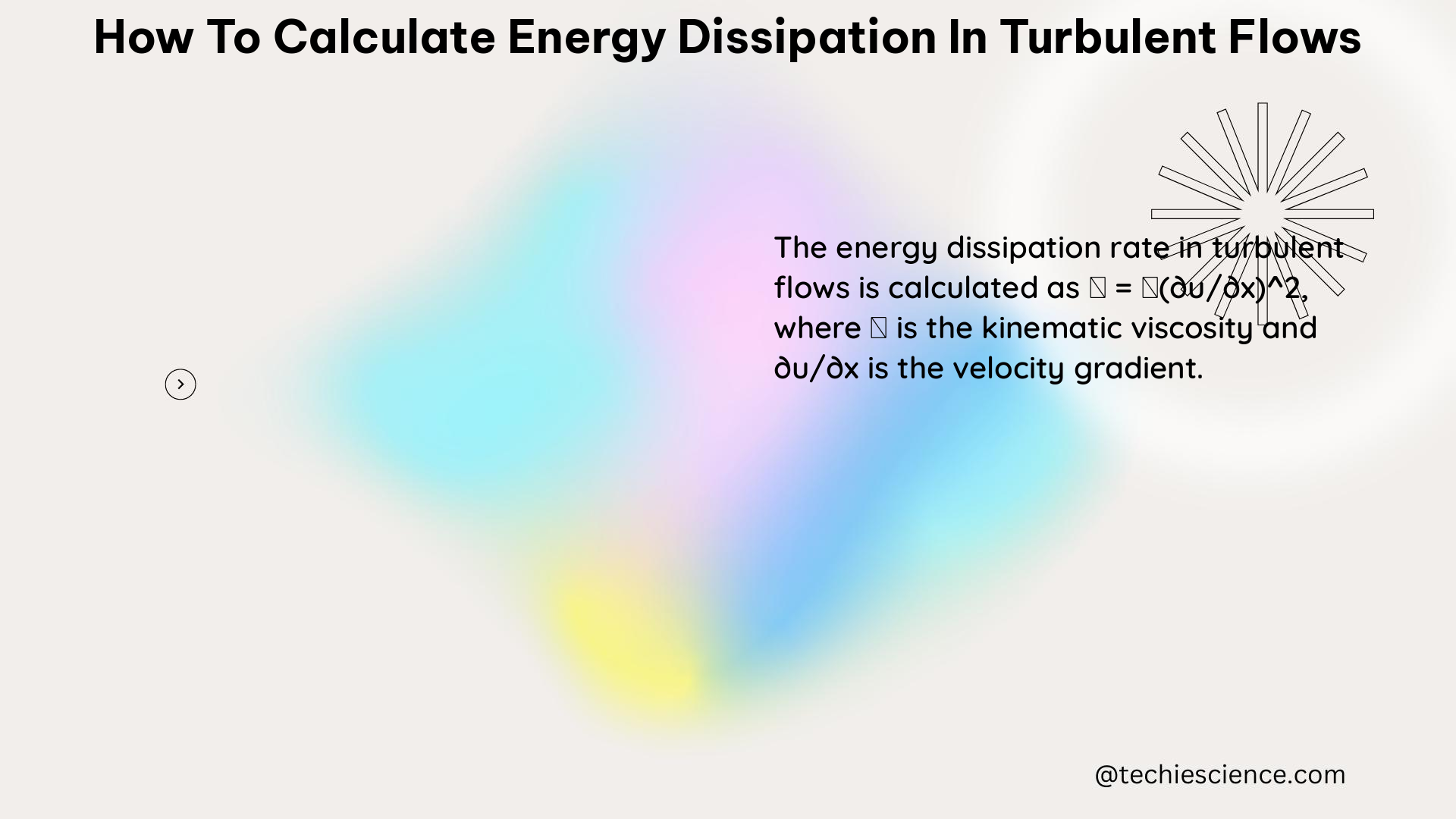
To calculate the TKE and its dissipation rate, we need to determine the turbulent intensity and the turbulent length scale. The turbulent intensity, denoted as I, is a measure of the magnitude of the turbulent fluctuations relative to the mean velocity. It is calculated as:

I = u_rms / U_mean

where u_rms is the root-mean-square of the velocity fluctuations, and U_mean is the mean velocity.

The turbulent length scale, L, is a measure of the size of the largest energy-containing eddies in the flow. It can be estimated based on the geometry of the flow and the turbulent intensity. For example, in a turbulent pipe flow, the turbulent length scale can be approximated as:

L = 0.07 * D

where D is the pipe diameter.

Calculating Energy Dissipation in Turbulent Pipe Flow

For turbulent pipe flow, the energy dissipation rate can be estimated using the well-known empirical relationship:

ε = (f/2) * (U^3 / D)

where:
– ε is the energy dissipation rate
– f is the Fanning friction factor, which can be obtained from empirical correlations or Moody diagrams
– U is the mean velocity of the fluid
– D is the pipe diameter

This formula provides a simple and practical way to estimate the energy dissipation rate in turbulent pipe flows, which is useful for various engineering applications, such as pressure drop calculations and heat transfer analysis.

Energy Dissipation in Multiphase Turbulent Flows

In the case of multiphase turbulent flows, such as oil-water mixtures, the energy dissipation process becomes more complex. Not all of the turbulent energy dissipates into heat; some of it is used for the breakup and coalescence of the dispersed phase (e.g., oil droplets).

The energy of the turbulent eddies plays a crucial role in the droplet dynamics. Smaller eddies can break up the droplets, while larger eddies contribute to the coalescence process. The balance between droplet breakup and coalescence determines the final droplet size distribution in the mixture.

Under certain conditions, such as low oil concentration and high energy dissipation rate, the coalescence process can be neglected, and the energy dissipation can be primarily attributed to the breakup of the dispersed phase.

Practical Applications and Numerical Examples

To illustrate the practical application of calculating energy dissipation in turbulent flows, let’s consider a numerical example:

Example: Turbulent Pipe Flow

Given:
– Pipe diameter, D = 0.1 m
– Mean velocity, U = 5 m/s
– Fluid density, ρ = 1000 kg/m³
– Fluid dynamic viscosity, μ = 0.001 Pa·s
– Fanning friction factor, f = 0.02

Calculate the energy dissipation rate, ε, in the turbulent pipe flow.

Solution:
1. Calculate the Reynolds number:
Re = ρ * U * D / μ = 1000 * 5 * 0.1 / 0.001 = 500,000 (turbulent flow)
2. Calculate the energy dissipation rate using the empirical formula:
ε = (f/2) * (U^3 / D) = (0.02/2) * (5^3 / 0.1) = 5 W/m³

This example demonstrates how to use the empirical relationship to estimate the energy dissipation rate in a turbulent pipe flow, which can be useful for various engineering applications, such as pressure drop calculations and heat transfer analysis.

Conclusion

Calculating energy dissipation in turbulent flows is a crucial aspect of understanding and optimizing the performance of various engineering systems. By leveraging the concepts of turbulent kinetic energy, turbulent intensity, and turbulent length scale, along with empirical relationships and numerical examples, this comprehensive guide provides a solid foundation for analyzing energy dissipation in both single-phase and multiphase turbulent flows. The insights gained from this guide can be applied to a wide range of engineering disciplines, from fluid mechanics to process engineering, to enhance the design and operation of complex systems.

References

1. Versteeg, H. K., & Malalasekera, W. (2007). An introduction to computational fluid dynamics: the finite volume method. Pearson education.
2. Pope, S. B. (2000). Turbulent flows. Cambridge university press.
3. Tennekes, H., & Lumley, J. L. (1972). A first course in turbulence. MIT press.
4. Hinze, J. O. (1975). Turbulence (Vol. 218). New York: McGraw-hill.
5. Kolmogorov, A. N. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Cr Acad. Sci. URSS, 30, 301-305.