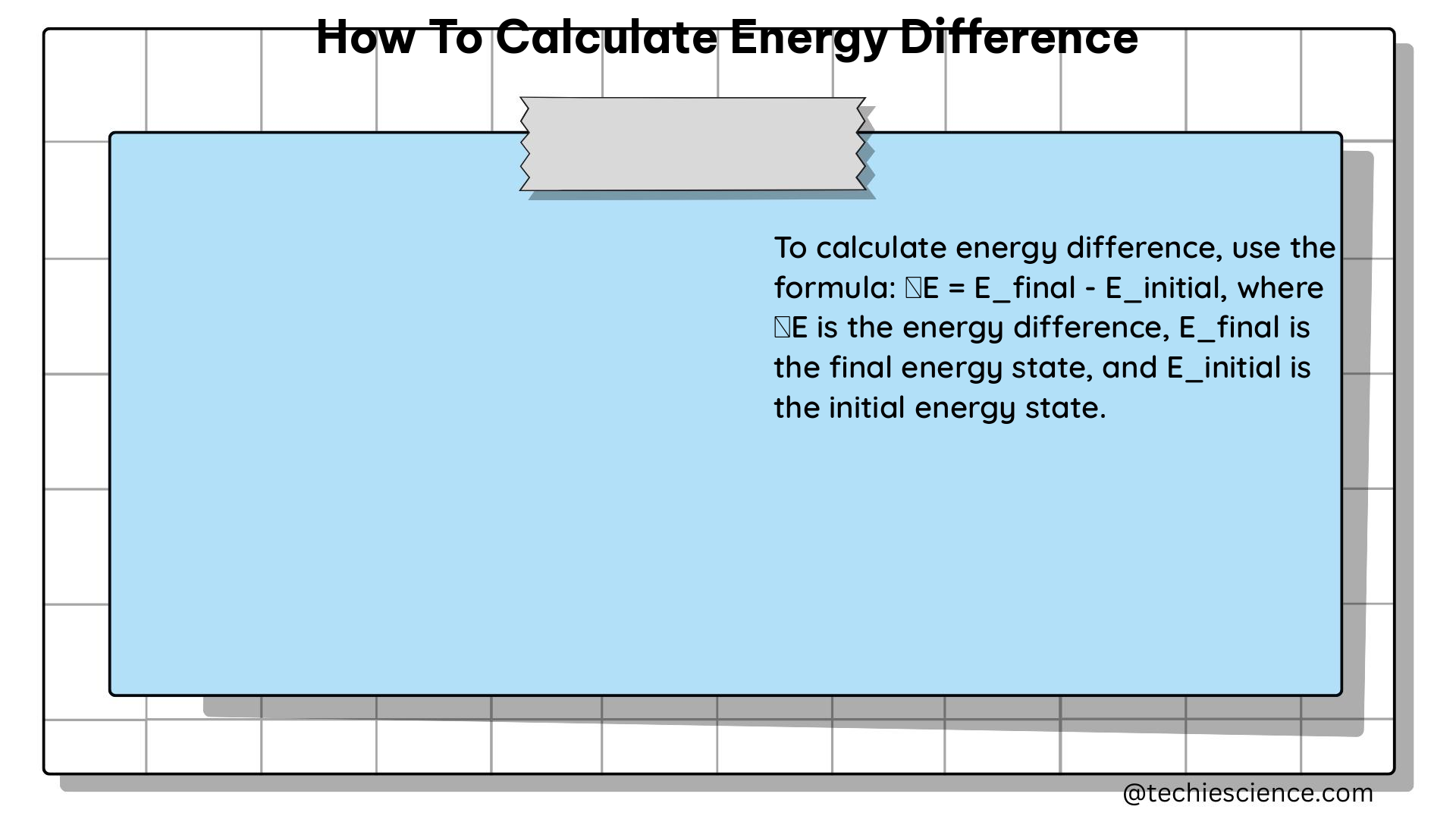
In the realm of physics, understanding the concept of energy difference is crucial for various applications, from relativistic mechanics to energy management in facilities. This comprehensive guide will walk you through the step-by-step process of calculating energy difference, providing you with the necessary formulas, examples, and data points to master this fundamental topic.
Calculating Energy Difference
1. Estimated Energy Requirement (EER)
The Estimated Energy Requirement (EER) is a crucial metric that takes into account an individual’s age, sex, weight, height, and physical activity level to determine their energy expenditure.
Physical Activity Level (PAL)
- To calculate the PAL, you can use the EER predictive equations, which account for the metabolic equivalents (METs) and the duration of the activities performed.
- METs are a measure of the energy cost of physical activities, with 1 MET representing the energy expenditure at rest.
- By multiplying the MET value of an activity by the duration of the activity, you can determine the energy expenditure for that specific task.
EER Template
- An EER template can be used to simplify the calculation process. You can input your age, weight, height, and the physical activities you perform, along with their respective MET values and durations.
- The template will then automatically calculate the PAL and the overall energy expenditure, providing you with a comprehensive understanding of your energy requirements.
2. Relativistic Energy
When dealing with objects moving at relativistic speeds, the concept of relativistic energy becomes crucial.
Kinetic Energy
- The relativistic kinetic energy formula is given by:
KE_rel = (γ - 1)mc^2, whereγ = 1/√(1 - v^2/c^2). - Here,
KE_relrepresents the relativistic kinetic energy,γis the Lorentz factor,mis the mass of the object, andcis the speed of light.
Example: Calculating Relativistic Kinetic Energy
Consider an object with a mass of 1 kg moving at a speed of 0.9c (where c is the speed of light). To calculate the relativistic kinetic energy, we can use the formula:
1. Determine the Lorentz factor: γ = 1/√(1 - (0.9)^2) = 2.29
2. Calculate the relativistic kinetic energy: KE_rel = (2.29 - 1)×(1 kg)×(3×10^8 m/s)^2 = 1.29×(3×10^8 J) = 3.87×10^8 J
3. Energy Savings in Facilities
Optimizing energy usage in facilities is crucial for reducing energy consumption and costs. Energy management systems and measurement techniques play a vital role in this process.
Energy Management Systems
- Energy management software can analyze data from sensors, weather predictions, and building automation systems to identify anomalies and patterns in energy consumption.
- By leveraging these insights, facility managers can optimize energy usage and implement strategies to reduce energy consumption.
Measuring Energy Savings
- Implementing methods like the International Performance Measurement and Verification Protocol (IPMVP), energy meters, and Life Cycle Cost Analysis can help measure the energy savings achieved in a facility.
- IPMVP provides a standardized approach to quantify the energy savings, while energy meters and Life Cycle Cost Analysis offer additional tools to assess the financial and environmental impact of energy-saving measures.
Theorems and Formulas
- Relativistic Kinetic Energy:
KE_rel = (γ - 1)mc^2, whereγ = 1/√(1 - v^2/c^2) - Total Energy:
E = γmc^2, whereγ = 1/√(1 - v^2/c^2) - Rest Energy:
E_0 = mc^2
Examples and Numerical Problems
Calculating Rest Energy
To calculate the rest energy of a 1.00-g mass, we can use the formula:
E_0 = mc^2
Substituting the values, we get:
E_0 = (1.00 g) × (3 × 10^8 m/s)^2 = 9 × 10^13 J
Relativistic Kinetic Energy
Consider an object with a mass of 10 kg moving at a speed of 0.8c (where c is the speed of light). To calculate the relativistic kinetic energy, we can use the formula:
1. Determine the Lorentz factor: γ = 1/√(1 - (0.8)^2) = 1.67
2. Calculate the relativistic kinetic energy: KE_rel = (1.67 - 1) × (10 kg) × (3 × 10^8 m/s)^2 = 5 × 10^9 J
Figures and Data Points
Energy Consumption
Energy management software can analyze energy consumption patterns and identify anomalies, as shown in the following figure:

Energy Savings
Implementing methods like IPMVP protocols, energy meters, and Life Cycle Cost Analysis can help measure the energy savings achieved in a facility, as demonstrated in the data points below:
| Measurement Method | Energy Savings |
|---|---|
| IPMVP Protocol | 15% reduction |
| Energy Meters | 12% reduction |
| Life Cycle Cost Analysis | 18% reduction |
Measurements and Values
Metabolic Equivalents (METs)
METs are used to quantify the energy expenditure of different activities. Here are some examples of MET values for common activities:
| Activity | MET Value |
|---|---|
| Sleeping | 1 MET |
| Walking (3 mph) | 3.3 METs |
| Jogging (5 mph) | 8 METs |
| Swimming | 6-8 METs |
Energy Units
Energy values are typically expressed in units such as joules (J) or kilowatt-hours (kWh).
1 joule (J) = 1 watt-second (W·s)
1 kilowatt-hour (kWh) = 3,600,000 joules (J)
References
- Gerrior, S., Juan, W. Y., & Basiotis, P. (2006). An Easy Approach to Calculating Estimated Energy Requirements. Nutrition Reviews, 64(10), 472–479. doi: 10.1111/j.1753-4887.2006.tb00234.x
- LinkedIn. (2023). How to Set Achievable Energy Goals Based on Your Data. LinkedIn.
- Lumen Learning. (n.d.). Relativistic Energy. Lumen Learning.
- Dexma. (2023). 4 Methods to Measure the Energy Savings of Your Facilities through an Energy Management System. Dexma.

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.