How to Calculate Center of Gravity: A Comprehensive Guide for Physics Students

The center of gravity (CoG) is a crucial concept in physics and engineering, representing the point where the weight of an object or system can be considered to act. Calculating the CoG allows for a better understanding of an object’s balance, stability, and overall behavior under external forces.

Understanding the Concept of Center of Gravity

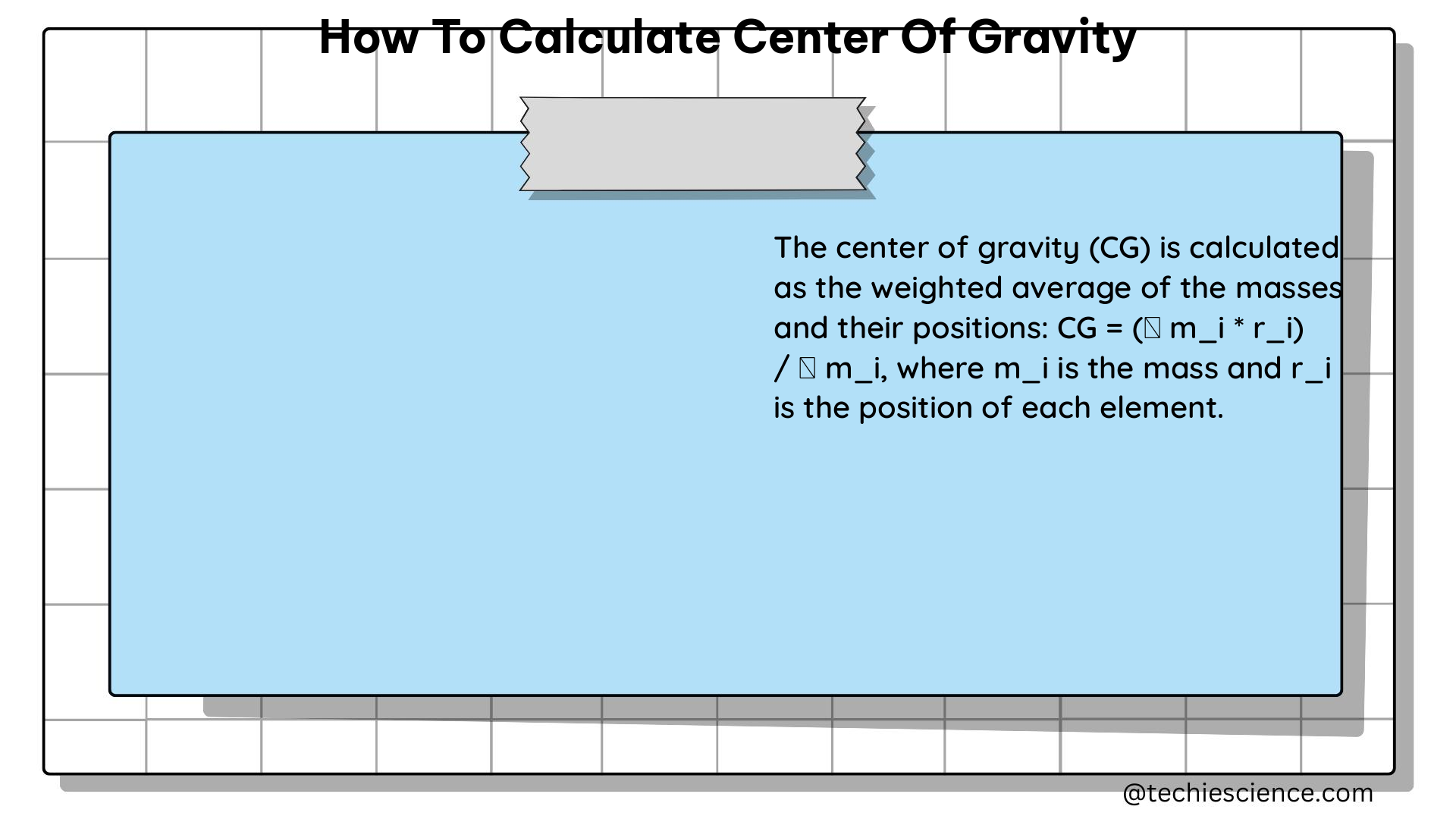
The center of gravity is defined as the weighted average of the positions of all the particles in a system. It is the point where the total weight of the object or system can be considered to act, and it is the point around which the object or system will balance if it is supported at that point.

The formula for calculating the center of gravity is:

CoG = (ΣD*W) / ΣW

Where:
– CoG is the center of gravity
– D is the distance from a reference point (datum)
– W is the weight of each object or part of the system
– ΣD*W is the sum of the moments (distance multiplied by weight)
– ΣW is the sum of the weights

Calculating the Center of Gravity for a 2D System

To calculate the center of gravity for a system of multiple objects on a 2D plane, follow these steps:

1. Determine the Mass and Position of Each Object: Identify the mass and coordinates (x, y) of each object in the system.

2. Calculate the Moments for Each Object: Multiply the mass of each object by its distance from the reference point (datum) to obtain the moment for that object.

3. Moment in the x-direction (Mx) = m * x

4. Moment in the y-direction (My) = m * y

5. Calculate the Total Moments and Total Weight: Sum the moments in the x-direction (ΣMx) and y-direction (ΣMy), as well as the total weight (ΣW).

6. ΣMx = Mx1 + Mx2 + Mx3 + … + Mxn
7. ΣMy = My1 + My2 + My3 + … + Myn

8. ΣW = m1 + m2 + m3 + … + mn

9. Calculate the Center of Gravity: Use the formula CoG = (ΣD*W) / ΣW to find the center of gravity.

10. CoGx = ΣMx / ΣW
11. CoGy = ΣMy / ΣW

Example Calculation

Let’s consider a system with four weights with the following properties:
– m1 = 2 kg, (x1, y1) = (0, 0)
– m2 = 5 kg, (x2, y2) = (2, 0)
– m3 = 0.5 kg, (x3, y3) = (2, 3)
– m4 = 3 kg, (x4, y4) = (4, 5)

1. Calculate the Moments for Each Object:
2. Mx1 = m1 * x1 = 2 * 0 = 0
3. My1 = m1 * y1 = 2 * 0 = 0
4. Mx2 = m2 * x2 = 5 * 2 = 10
5. My2 = m2 * y2 = 5 * 0 = 0
6. Mx3 = m3 * x3 = 0.5 * 2 = 1
7. My3 = m3 * y3 = 0.5 * 3 = 1.5
8. Mx4 = m4 * x4 = 3 * 4 = 12

9. My4 = m4 * y4 = 3 * 5 = 15

10. Calculate the Total Moments and Total Weight:

11. ΣMx = Mx1 + Mx2 + Mx3 + Mx4 = 0 + 10 + 1 + 12 = 23
12. ΣMy = My1 + My2 + My3 + My4 = 0 + 0 + 1.5 + 15 = 16.5

13. ΣW = m1 + m2 + m3 + m4 = 2 + 5 + 0.5 + 3 = 10.5

14. Calculate the Center of Gravity:

15. CoGx = ΣMx / ΣW = 23 / 10.5 ≈ 2.2
16. CoGy = ΣMy / ΣW = 16.5 / 10.5 ≈ 1.58

Therefore, the center of gravity for this system is approximately at the coordinates (CoGx, CoGy) ≈ (2.2, 1.58).

Factors to Consider when Calculating the Center of Gravity

1. Consistent Datum: Choose a consistent reference point (datum) when calculating the distances for each object.
2. Unit Consistency: Ensure that the weights and distances are in the same units to avoid errors in the calculation.
3. Symmetry and Homogeneity: For symmetric or homogeneous objects, the center of gravity may coincide with the geometric center.
4. Irregular Shapes: For objects with irregular shapes, the center of gravity may not be easily determined and may require more advanced techniques, such as using integration or numerical methods.
5. 3D Systems: The principles for calculating the center of gravity can be extended to 3D systems, where the moments and weights are calculated in all three dimensions (x, y, z).

Practical Applications of Center of Gravity Calculations

Knowing the center of gravity of an object or system is crucial in various fields, such as:

1. Structural Engineering: Determining the stability and balance of structures, buildings, and bridges.
2. Mechanical Engineering: Designing and analyzing the behavior of machines, vehicles, and other mechanical systems.
3. Aerospace Engineering: Calculating the center of gravity of aircraft, spacecraft, and their payloads for stability and control.
4. Robotics: Ensuring the stability and balance of robotic systems, especially for mobile robots.
5. Sports and Recreation: Analyzing the center of gravity of sports equipment, such as bicycles, skis, and golf clubs, to optimize performance.

Conclusion

Calculating the center of gravity is a fundamental skill for physics students and professionals in various engineering fields. By understanding the principles and applying the step-by-step process outlined in this guide, you can accurately determine the center of gravity of complex systems, leading to a better understanding of their balance, stability, and behavior under external forces.

References

1. Stelling Consulting. (n.d.). Centers of Gravity Calculator. Retrieved from https://www.stellingconsulting.nl/Centers_of_gravity_calculator.php
2. LGH. (2022, March 17). How To: Easily Find Center of Gravity for Your Load. Retrieved from https://rentlgh.com/blog/how-to-easily-find-center-of-gravity-for-your-load/
3. Study.com. (2021, October 25). How to Find the Center of Mass of Multiple Objects on a 2D Plane. Retrieved from https://study.com/skill/learn/how-to-find-the-center-of-mass-of-multiple-objects-on-a-2d-plane-explanation.html
4. wikiHow. (2024, May 10). 5 Ways to Calculate Center of Gravity. Retrieved from https://www.wikihow.com/Calculate-Center-of-Gravity
5. Raptor Scientific. (n.d.). Accurately Measure Center of Gravity. Retrieved from https://raptor-scientific.com/resources/center-of-gravity/