The relationship between electric and magnetic fields is a fundamental concept in physics, described by Maxwell’s equations. The idea that a changing electric field produces a magnetic field is encapsulated in Faraday’s law of electromagnetic induction, which states that a changing magnetic field induces an electromotive force (EMF) in a closed loop of wire. This EMF, in turn, generates an electric field.
Understanding the Relationship between Electric and Magnetic Fields
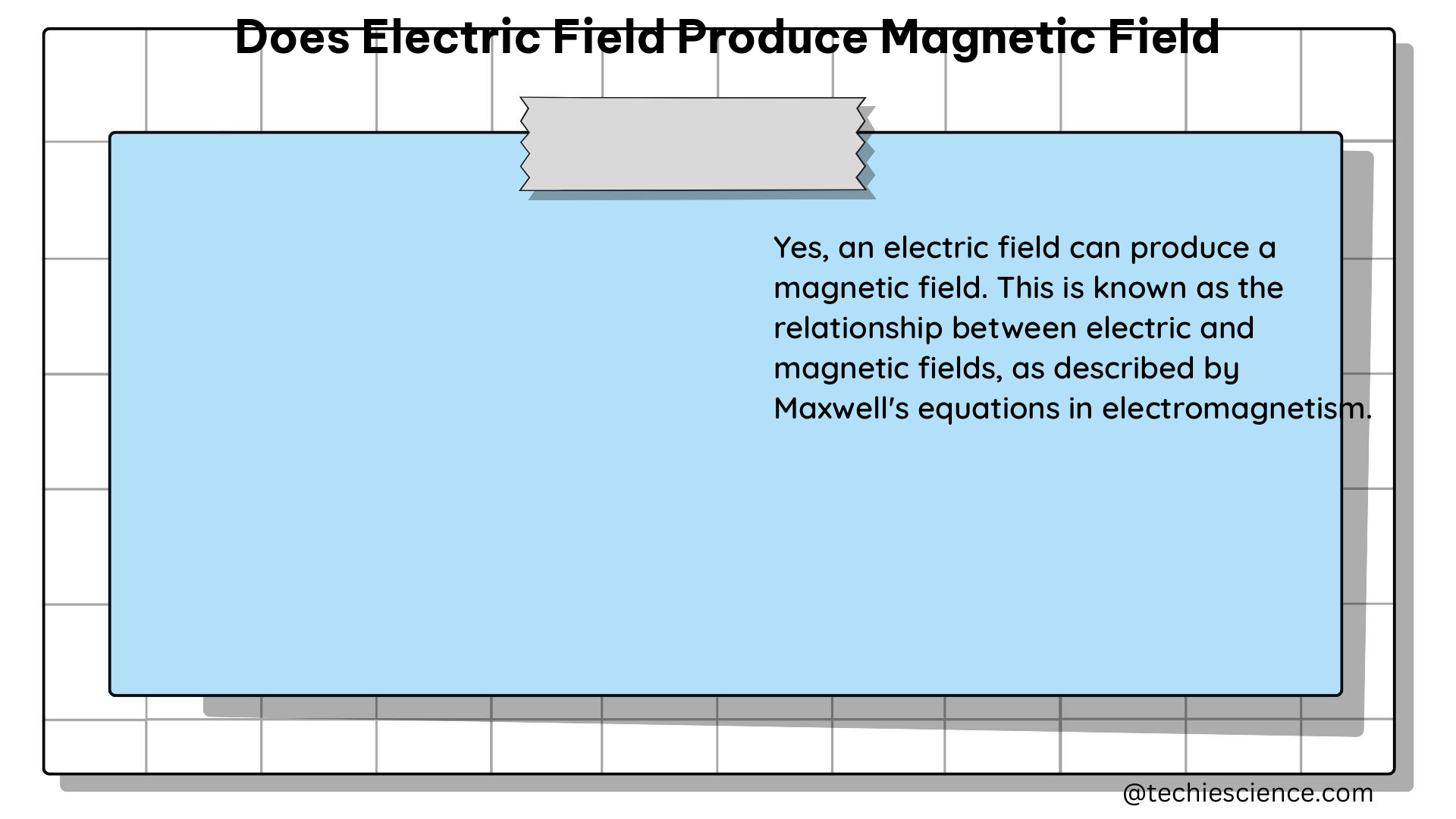
The connection between electric and magnetic fields is a crucial aspect of electromagnetism, which is one of the four fundamental forces in nature. This relationship is governed by Maxwell’s equations, a set of four equations that describe the behavior of electric and magnetic fields.
Maxwell’s Equations
- Gauss’s Law for Electric Fields: The electric flux through any closed surface is proportional to the total electric charge enclosed by that surface.
- Gauss’s Law for Magnetic Fields: The magnetic flux through any closed surface is always zero, meaning that magnetic monopoles do not exist.
- Faraday’s Law of Electromagnetic Induction: A changing magnetic field induces an electromotive force (EMF) in a closed loop of wire, which in turn generates an electric field.
- Ampère’s Law with Maxwell’s Correction: A changing electric field produces a magnetic field, and this magnetic field is proportional to the rate of change of the electric field.
These equations demonstrate the fundamental connection between electric and magnetic fields, and they form the basis for our understanding of electromagnetic phenomena.
Faraday’s Law of Electromagnetic Induction
Faraday’s law of electromagnetic induction is the key to understanding how a changing electric field can produce a magnetic field. The law states that a changing magnetic field induces an electromotive force (EMF) in a closed loop of wire, which in turn generates an electric field.
The mathematical expression of Faraday’s law is:
EMF = -N * dΦ/dt
Where:
– EMF is the electromotive force (in volts)
– N is the number of turns in the coil
– dΦ is the change in magnetic flux (in webers)
– dt is the change in time (in seconds)
The negative sign in the equation indicates that the induced EMF opposes the change in the magnetic field, a principle known as Lenz’s law.
Experimental Demonstration of Electromagnetic Induction
To illustrate the relationship between electric and magnetic fields, we can consider a simple experiment involving a solenoid (coil of wire) and a magnet.
Experimental Setup
- Solenoid: A coil of wire with a large number of turns, typically made of copper wire.
- Magnet: A permanent magnet or an electromagnet that can produce a changing magnetic field.
- Multimeter: An instrument used to measure the induced current or voltage in the solenoid.
Experimental Procedure
- Place the solenoid in a stable position.
- Bring the magnet close to the solenoid and move it back and forth, creating a changing magnetic field.
- Observe the multimeter connected to the solenoid. It will display a reading, indicating that an electric current has been induced in the solenoid.
Experimental Observations
- The induced current in the solenoid is proportional to the rate of change of the magnetic field.
- The direction of the induced current is such that it opposes the change in the magnetic field, as described by Lenz’s law.
- The strength of the induced current can be measured using the multimeter, providing a quantifiable measure of the relationship between the changing magnetic field and the induced electric field.
Numerical Example
Let’s consider a numerical example to illustrate the concept further.
Suppose we have a solenoid with 500 turns, placed in a magnetic field of 0.5 Tesla. If the magnetic field is changing at a rate of 0.1 Tesla per second, what is the induced EMF in the solenoid?
Using Faraday’s law, we can calculate the EMF as:
EMF = -N * dΦ/dt
EMF = -500 * (0.1/1)
EMF = -50 Volts
The negative sign indicates that the direction of the induced current opposes the change in the magnetic field, as per Lenz’s law.
Graphical Representation of Electromagnetic Induction
The relationship between electric and magnetic fields can be visualized using vector field diagrams and animations.
Magnetic Field Representation
The magnetic field can be represented as a vector field, with lines indicating the direction and strength of the field. The density of these lines represents the intensity of the magnetic field.
Changing Magnetic Field Animation
An animation can be used to show the movement of the magnetic field lines over time, illustrating the concept of a changing magnetic field. This can help visualize how the changing magnetic field induces an electric field in a closed loop of wire.
Conclusion
The relationship between electric and magnetic fields is a fundamental concept in physics, governed by Maxwell’s equations. Faraday’s law of electromagnetic induction is the key to understanding how a changing electric field can produce a magnetic field. The simple experiment with a solenoid and a magnet demonstrates this principle, and the numerical example provides a quantitative understanding of the induced EMF.
By understanding the technical details, physics formulas, and experimental observations related to the production of magnetic fields by electric fields, students can develop a deeper appreciation for the underlying principles of electromagnetism.
Reference:
- Maxwell’s Equations – Encyclopedia Britannica
- Faraday’s Law of Induction – HyperPhysics
- Electromagnetic Induction – Khan Academy
Hi..I am Indrani Banerjee. I completed my bachelor’s degree in mechanical engineering. I am an enthusiastic person and I am a person who is positive about every aspect of life. I like to read Books and listen to music.