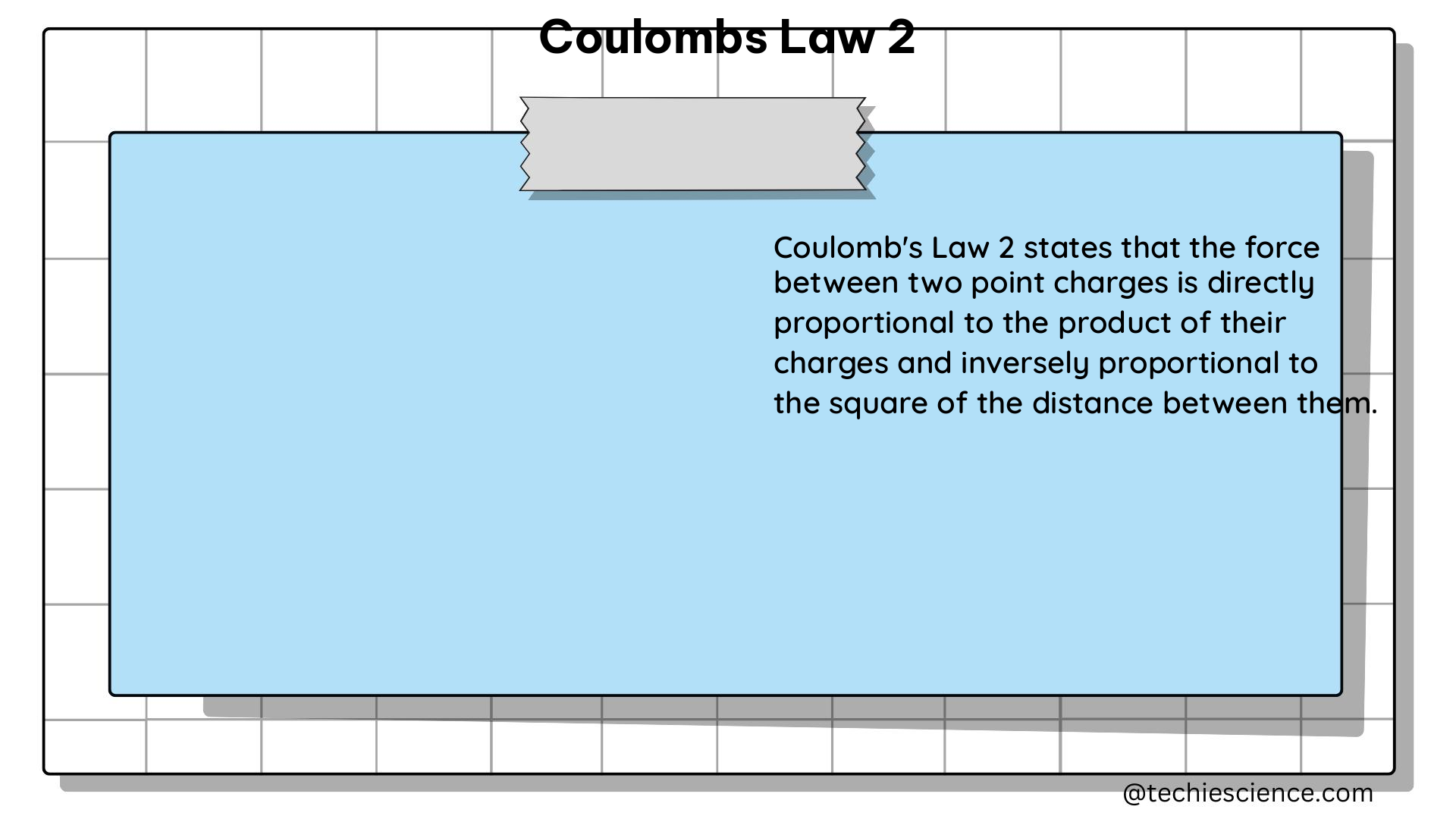
Coulomb’s Law 2: A Comprehensive Guide for Science Students

Coulomb’s Law is a fundamental principle in physics that describes the force between two charged particles. The law states that the force (F) between two charges (q1 and q2) is directly proportional to the product of their charges and inversely proportional to the square of the distance (r) between them. Mathematically, it can be represented as F = k * q1 * q2 / r^2, where k is a proportionality constant equal to 9 x 10^9 Nm^2/C^2.

Understanding the Theorem and Formula

Coulomb’s Law can be expressed mathematically as:

F = k * (q1 * q2) / r^2

Where:
– F is the force of interaction between the two charges (in Newtons, N)
– q1 and q2 are the magnitudes of the two charges (in Coulombs, C)
– r is the distance between the two charges (in meters, m)
– k is the Coulomb constant, which has a value of 8.99 × 10^9 N⋅m^2/C^2

The Coulomb constant, k, is a fundamental physical constant that represents the strength of the electrostatic force between two point charges. It is a dimensionful constant, with units of N⋅m^2/C^2, which reflects the fact that the electrostatic force is an inverse-square force, just like the gravitational force.

Physics Examples and Applications

1. Charged Particles in an Electric Field: Coulomb’s Law can be used to calculate the force between two charged particles, such as an electron and a proton, or two electrons. This is particularly important in understanding the behavior of charged particles in an electric field.

2. Atomic and Molecular Structure: Coulomb’s Law plays a crucial role in understanding the structure and stability of atoms and molecules. The electrostatic forces between the positively charged nucleus and the negatively charged electrons, as well as the forces between the electrons themselves, are all governed by Coulomb’s Law.

3. Electrostatic Attraction and Repulsion: Coulomb’s Law explains the phenomenon of electrostatic attraction and repulsion, where like charges (positive-positive or negative-negative) repel each other, while unlike charges (positive-negative) attract each other.

4. Electrical Circuits: Coulomb’s Law is fundamental to understanding the behavior of electrical circuits, as it governs the flow of electric current and the distribution of charges within the circuit.

5. Particle Accelerators: Coulomb’s Law is crucial in the design and operation of particle accelerators, such as the Large Hadron Collider (LHC), where charged particles are accelerated and collided at high energies to study the fundamental properties of matter.

6. Astrophysics and Cosmology: Coulomb’s Law is also relevant in astrophysics and cosmology, as it describes the electrostatic forces between charged particles in the universe, which can influence the behavior of celestial bodies and the evolution of the cosmos.

Chemistry Equations and Numerical Problems

1. Calculating the Force between Two Charges: Given two point charges, q1 and q2, separated by a distance r, the force between them can be calculated using the Coulomb’s Law formula:

F = k * (q1 * q2) / r^2

Example: Two point charges, q1 = 2 μC and q2 = -3 μC, are separated by a distance of 0.5 m. Calculate the force between them.

Solution:
Given:
– q1 = 2 μC = 2 × 10^-6 C
– q2 = -3 μC = -3 × 10^-6 C
– r = 0.5 m
– k = 8.99 × 10^9 N⋅m^2/C^2

Substituting the values in the Coulomb’s Law formula:
F = (8.99 × 10^9 N⋅m^2/C^2) * [(2 × 10^-6 C) * (-3 × 10^-6 C)] / (0.5 m)^2
F = -1.078 × 10^-3 N

The negative sign indicates that the force is attractive, as the charges have opposite signs.

1. Calculating the Electric Field Strength: Coulomb’s Law can also be used to calculate the electric field strength at a point due to a point charge. The electric field strength, E, is given by:

E = k * q / r^2

Example: Calculate the electric field strength at a point 2 m away from a point charge of 5 μC.

Solution:
Given:
– q = 5 μC = 5 × 10^-6 C
– r = 2 m
– k = 8.99 × 10^9 N⋅m^2/C^2

Substituting the values in the formula:
E = (8.99 × 10^9 N⋅m^2/C^2) * (5 × 10^-6 C) / (2 m)^2
E = 1.124 × 10^3 N/C

1. Calculating the Potential Energy of a Charge System: Coulomb’s Law can be used to calculate the potential energy of a system of charges. The potential energy, U, between two charges q1 and q2 separated by a distance r is given by:

U = k * (q1 * q2) / r

Example: Calculate the potential energy between two charges of 3 μC and -2 μC separated by a distance of 0.3 m.

Solution:
Given:
– q1 = 3 μC = 3 × 10^-6 C
– q2 = -2 μC = -2 × 10^-6 C
– r = 0.3 m
– k = 8.99 × 10^9 N⋅m^2/C^2

Substituting the values in the formula:
U = (8.99 × 10^9 N⋅m^2/C^2) * [(3 × 10^-6 C) * (-2 × 10^-6 C)] / (0.3 m)
U = -1.799 × 10^-3 J

The negative sign indicates that the potential energy is attractive, as the charges have opposite signs.

Figures and Data Points

Figure 1: Illustration of Coulomb’s Law, showing the force of interaction between two point charges.

Data Points:
– Coulomb constant, k = 8.99 × 10^9 N⋅m^2/C^2
– Charge of an electron, e = -1.6 × 10^-19 C
– Charge of a proton, p = +1.6 × 10^-19 C
– Mass of an electron, m_e = 9.11 × 10^-31 kg
– Mass of a proton, m_p = 1.67 × 10^-27 kg

Conclusion

Coulomb’s Law is a fundamental principle in physics that describes the force between two charged particles. It is a powerful tool for understanding the behavior of charged particles in various contexts, from atomic and molecular structures to electrical circuits and particle accelerators. By mastering the theorem, formula, and applications of Coulomb’s Law, science students can gain a deeper understanding of the underlying principles governing the interactions between charged objects.

References:

1. Coulomb’s Law – GeeksforGeeks: https://www.geeksforgeeks.org/problems-based-on-coulombs-law/
2. Coulomb’s Law – The Physics Classroom: https://www.physicsclassroom.com/class/estatics/Lesson-3/Coulomb-s-Law
3. Coulomb’s Law Explained – YouTube: https://www.youtube.com/watch?v=yUPdtFqilXo
4. Coulomb’s Law – Wikipedia: https://en.wikipedia.org/wiki/Coulomb%27s_law
5. Fundamental Physical Constants – NIST: https://physics.nist.gov/cuu/Constants/index.html