Coulomb’s law is a fundamental principle in physics and chemistry that describes the force between charged particles. The law states that the force (F) between two charges (q1 and q2) is directly proportional to the product of the charges and inversely proportional to the square of the distance (r) between them. This can be represented mathematically as F = k * (q1 * q2) / r^2, where k is a proportionality constant equal to 1/4πε0, and ε0 is the permittivity of free space.
Understanding the Fundamentals of Coulomb’s Law
Coulomb’s Law Theorem
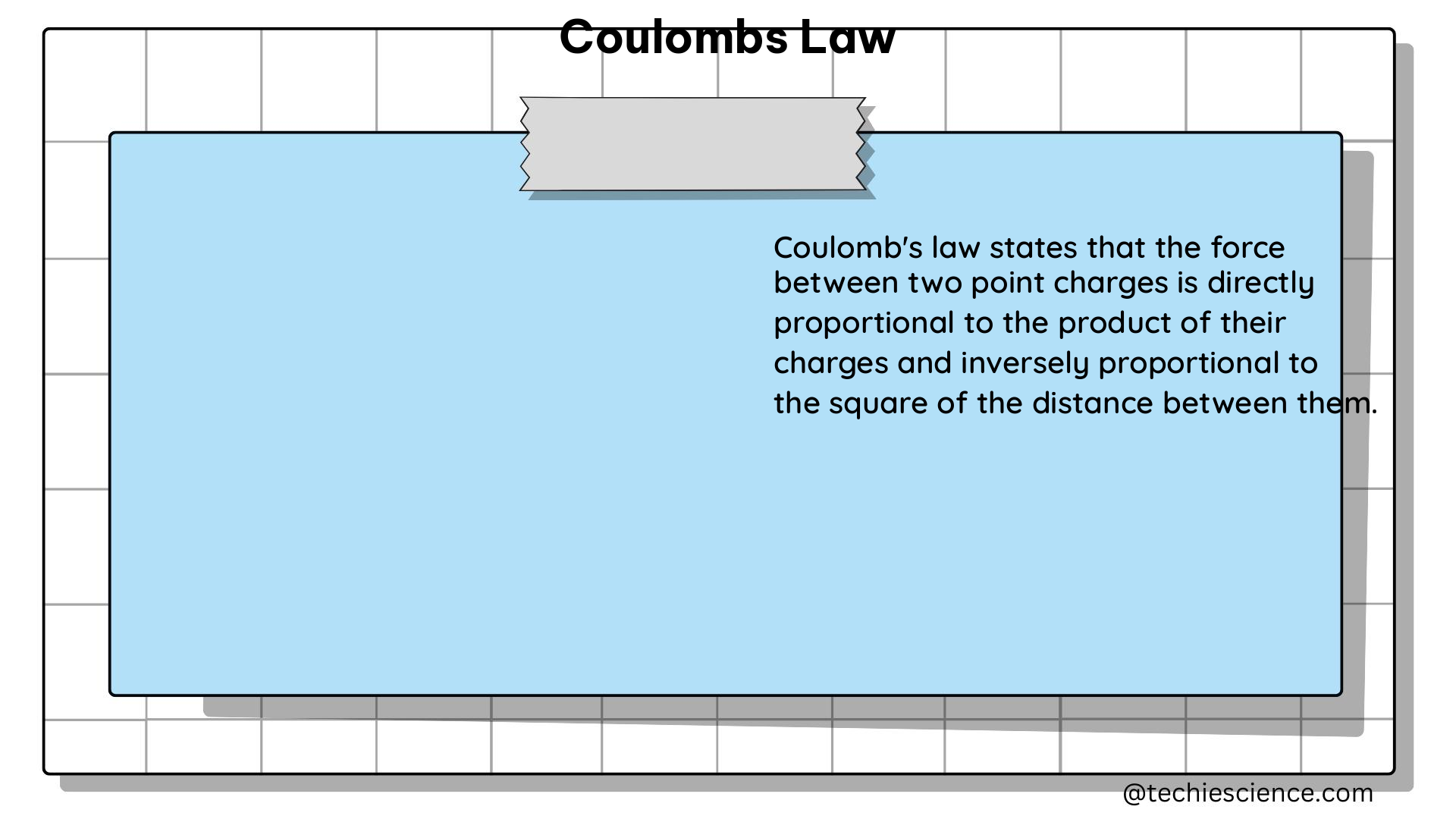
Coulomb’s law states that the force of interaction between two point charges is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them.
Mathematically, Coulomb’s law can be expressed as:
F = k * (q1 * q2) / r^2
Where:
– F is the force of interaction between the two charges (in newtons, N)
– q1 and q2 are the magnitudes of the two charges (in coulombs, C)
– r is the distance between the two charges (in meters, m)
– k is the Coulomb constant, which is equal to 8.99 × 10^9 N⋅m^2/C^2 in the SI system of units
Coulomb Constant (k)
The Coulomb constant, also known as the electrostatic constant or the electric force constant, is a physical constant that appears in Coulomb’s law. It is a measure of the strength of the electrostatic force between two point charges.
The value of the Coulomb constant in the SI system of units is:
k = 8.99 × 10^9 N⋅m^2/C^2
This constant is used to calculate the force between two charged particles in a vacuum or in a medium with a relative permittivity of 1.
Permittivity of Free Space (ε0)
The permittivity of free space, also known as the electric constant or the vacuum permittivity, is a physical constant that represents the ability of a vacuum to support an electric field. It is a fundamental constant in electromagnetism and is used in the calculation of the Coulomb constant.
The value of the permittivity of free space in the SI system of units is:
ε0 = 8.854 × 10^-12 F/m
This constant is used to calculate the Coulomb constant as follows:
k = 1 / (4π * ε0)
Applications of Coulomb’s Law
Calculating the Force Between Charged Particles
Coulomb’s law can be used to calculate the force between two charged particles. For example, if you have two point charges with magnitudes of 2 μC and 3 μC, and they are separated by a distance of 0.5 m, you can use Coulomb’s law to calculate the force between them:
F = k * (q1 * q2) / r^2
F = (8.99 × 10^9 N⋅m^2/C^2) * ((2 × 10^-6 C) * (3 × 10^-6 C)) / (0.5 m)^2
F = 2.16 × 10^-3 N
This force can be either attractive or repulsive, depending on the signs of the charges.
Calculating the Force Between Charged Particles in Atoms and Molecules
Coulomb’s law is also used to calculate the force between charged particles in atoms and molecules, which is crucial in understanding chemical bonding and the behavior of chemical systems. For example, in a water molecule (H2O), the oxygen atom has a partial negative charge, while the hydrogen atoms have partial positive charges. Coulomb’s law can be used to calculate the attractive force between the oxygen and hydrogen atoms, which contributes to the formation of the covalent bonds in the molecule.
Designing Electrical Circuits and Devices
Coulomb’s law has practical applications in electrical engineering and electronics. The law is used in the design of electrical circuits and devices, such as capacitors and transformers, which are essential components in many electronic devices. By understanding the force between charged particles, electrical engineers can design more efficient and reliable electrical systems.
Calculating Capacitance and Energy Stored in Capacitors
Coulomb’s law is also used in the calculation of the capacitance of electrical components and the energy stored in capacitors. The capacitance of a capacitor is a measure of the amount of charge it can store, and it is directly proportional to the area of the plates and inversely proportional to the distance between them. Coulomb’s law can be used to calculate the force between the plates of a capacitor, which is related to the energy stored in the capacitor.
Numerical Problems and Examples
Example 1: Calculating the Force Between Two Charges
Two point charges, q1 = 3 μC and q2 = -2 μC, are separated by a distance of 0.1 m. Calculate the force between the two charges.
Given:
– q1 = 3 μC = 3 × 10^-6 C
– q2 = -2 μC = -2 × 10^-6 C
– r = 0.1 m
Using Coulomb’s law:
F = k * (q1 * q2) / r^2
F = (8.99 × 10^9 N⋅m^2/C^2) * ((3 × 10^-6 C) * (-2 × 10^-6 C)) / (0.1 m)^2
F = -5.39 × 10^-3 N
The negative sign indicates that the force is attractive.
Example 2: Calculating the Force Between Charged Particles in a Water Molecule
In a water molecule (H2O), the oxygen atom has a partial negative charge of -0.34e, and the hydrogen atoms have partial positive charges of +0.17e each, where e is the elementary charge (1.602 × 10^-19 C). Assuming the distance between the oxygen and hydrogen atoms is 0.096 nm, calculate the force of attraction between the oxygen and one of the hydrogen atoms.
Given:
– q1 = -0.34e = -0.544 × 10^-19 C
– q2 = +0.17e = 0.272 × 10^-19 C
– r = 0.096 nm = 9.6 × 10^-11 m
Using Coulomb’s law:
F = k * (q1 * q2) / r^2
F = (8.99 × 10^9 N⋅m^2/C^2) * ((0.544 × 10^-19 C) * (0.272 × 10^-19 C)) / (9.6 × 10^-11 m)^2
F = -5.52 × 10^-10 N
The negative sign indicates that the force is attractive.
Example 3: Calculating the Capacitance and Energy Stored in a Capacitor
A parallel-plate capacitor has a plate area of 0.2 m^2 and a separation distance of 0.5 mm. Calculate the capacitance of the capacitor and the energy stored in the capacitor when it is charged to a potential difference of 100 V.
Given:
– A = 0.2 m^2
– d = 0.5 mm = 0.0005 m
– V = 100 V
Calculating the capacitance:
C = ε0 * A / d
C = (8.854 × 10^-12 F/m) * (0.2 m^2) / (0.0005 m)
C = 3.54 × 10^-9 F
Calculating the energy stored in the capacitor:
U = 0.5 * C * V^2
U = 0.5 * (3.54 × 10^-9 F) * (100 V)^2
U = 1.77 × 10^-5 J
Conclusion
Coulomb’s law is a fundamental principle in physics and chemistry that describes the force between charged particles. By understanding the mathematical formulation of Coulomb’s law and the associated constants, such as the Coulomb constant and the permittivity of free space, you can solve a wide range of problems related to the behavior of charged particles in various contexts, including atoms, molecules, electrical circuits, and capacitors.
The examples and numerical problems provided in this guide demonstrate the practical applications of Coulomb’s law and how it can be used to calculate the force between charged particles, the capacitance and energy stored in capacitors, and the interactions between charged particles in chemical systems. By mastering Coulomb’s law, you can deepen your understanding of electrostatics and apply it to solve complex problems in physics, chemistry, and electrical engineering.
References:
- “Coulomb’s Law – Physics Tutorial” – The Physics Classroom
- “How did Coulomb measure charges?” – Physics Stack Exchange
- “Coulomb’s law | Definition & Facts” – Britannica
- “Problems Based on Coulomb’s Law” – GeeksforGeeks
- “Permittivity of free space” – Wikipedia
- “Capacitance” – Khan Academy

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.