List of Content
- Continuity equation
- Continuity equation differential form
- Continuity equation for incompressible flow
- Continuity equation for two-dimensional coplanar flow
- Continuity equation example
- Question & Answers
- MCQ
- Conclusion
Continuity equation
The fluid flowing through the stream tube is assumed to the ideal fluid. There is no flow occurs across the streamline. It means that fluid enters at one end and leave at the other end there is no in-between outlet. Consider flow condition at inlet cross-section 1-1 as below,
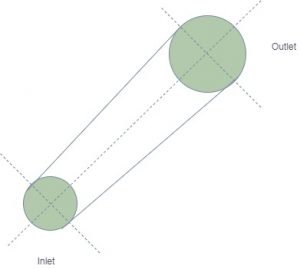
| Parameters | Inlet section 1-1 | Outlet section 2-2 |
| Cross-sectional area | A | A+dA |
| Average fluid density | ? | ?+d? |
| Mean flow velocity | V | V+dV |
The fluid mass which flows between this two considered sections is given by following formula,
dm = (A V ? dt ) – ( A + dA ) ( V+ dV ) ( ? + d? ) dt Eq … 1
by simplifying above equation we get ,
dm/dt = – (A V d? + V ? dA + A ? dV) Eq … 2
As we know that steady flow means constant mass flow rate, it means here dm/dt = 0. Now Eq. 2 turned as below,
(A V d? + V ? dA + A ? dV) = 0 Eq … 3
Now, divide Eq. 3 with ? A V, equation will be like,
( d?/? ) + ( dA/A ) + ( dV/V ) = 0 Eq … 4
d ( ? A V ) = 0 Eq … 5
? A V = Constant Eq … 6
Here, the Eq. 6 makes us know that the mass of fluid passing through stream tube is constant at every section.
Suppose the fluid is incompressible (liquid) then the density of fluid will not change at any point. It means that fluid density is constant.
A V = Constant
A1 V1 = A2 V2 Eq … 7
Eq. 7 represents the continuity equation for steady incompressible flow inside the stream tube. The continuity equation gives a basic understanding of area and velocity. The cross-sectional area’s change affects the velocity of flow inside the stream tube, pipe, hollow channel, etc. Here, the exciting thing is a product of velocity and cross-sectional area. This product is constant at any point in the stream tube. The velocity is inversely proportionate to the cross-section area of the stream tube or pipe.
Continuity equation differential form
To derive the differential form of the continuity equation, consider an object as shown in the figure. The dimensions are dx, dy, and dz. There are some assumptions for this formation. The mass of fluid is not created or destroyed, no cavity or bubbles in fluid ( continuous flow). We consider dx in the x-direction, dy in y, and dz in z directions for easiness in derivation.
If u is the velocity of fluid flow as per shown face in the figure. It is assumed that velocity is uniform throughout the face cross-sectional area. The fluid velocity at surface 1-2-3-4 is u. now; the surface 5-6-7-8 is a dx distance far from 1-2-3-4. So, the velocity at 5-6-7-8 is given as
u+∂u/∂x dx
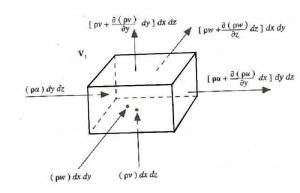
As we know that there change in density by using compressible fluid. If the compressible fluid passes through an object, the density will change.
The mass flow entering the object is given as
Mass flow = ? A V
Mass flow rate = ? A V dt
The fluid entering on 1-2-3-4
Inlet fluid = density ( area * velocity) dt
Inlet fluid= ρ u dy dz dt
Eq … 1
The fluid leaving from 5-6-7-8
Outlet fluid
outlet fluid= [ρu+ ∂/∂x (ρu)dx] dy dz dtt
Eq … 2
Now, the difference between inlet fluid and outlet fluid is mass stayed in x direction flow.
= ρ u dy dz dt- [ρu+ ∂/∂x (ρu)dx] dy dz dt
= - ∂/∂x (ρu)dx dy dz dt
Eq … 3
Similarly, we consider mass of fluid in y and z direction is given as below,
= - ∂/∂y (ρv)dx dy dz dt
Eq … 4
= - ∂/∂z (ρw)dx dy dz dt
Eq … 5
Here, the v and w are the velocities of fluid in y and z directions, respectively.
For the mass flow of fluid in all three directions, axes are given by the addition of Eq. 3, 4, and 5. It is given as below total fluid mass,
= -[∂/∂x (ρu)+ ∂/∂y (ρv)+ ∂/∂z (ρw)] dx dy dz dt
Eq … 6
The rate of change of mass within the object is given by,
∂m/∂t dt= ∂/∂t ( ρ ×volume ) dt= ∂ρ/∂t dx dy dz dt
Eq … 7
As per understanding of mass conservation Eq. 6 equal to Eq. 7
-[∂/∂x (ρu)+ ∂/∂y (ρv)+ ∂/∂z (ρw)] dx dy dz dt= ∂ρ/∂t dx dy dz dt
Solving the above equation and simplifying it, we get,
∂ρ/∂t+∂/∂x (ρu)+ ∂/∂y (ρv)+ ∂/∂z (ρw)=0
Eq … 8
Eq. 8 is. Continuity equation for general flow. It may be steady or unsteady, compressible or incompressible.
Continuity equation for incompressible flow
If we consider flow is steady and incompressible. We know that in the case of steady flow ??/?t = 0. If the flow is incompressible, then density ? remains constant. So, by considering this condition, Eq. 8 can be written as,
∂u/∂x+ ∂v/∂y + ∂w/∂z =0
Continuity equation for two-dimensional coplanar flow
In two-dimensional flow, there are two directions x and y. So, u velocity in x-direction and v velocity in the y-direction. There is no z-direction, so velocity in the z-direction is zero. By considering these conditions, the Eq. 8 turned as below,
∂/∂x (ρu)+ ∂/∂y (ρv)=0
Compressible flow
∂u/∂x+ ∂v/∂y =0
Incompressible flow, Density is zero
Continuity equation example
There is flow air through the pipe at the rate of 0.25 kg/s at an absolute pressure of 2.25 bar and temperature of 300 K. If the flow velocity is 7.5 m/s, then what will be the pipe’s minimum diameter?
Data,
m = 0.25 kg/s,
P = 2.25 bar,
T = 300 K,
V = 7.5 m/s,
Calculate the density of air,
P = ? R T
? = P / RT
? = ( 2.25 * 105 )/ ( 287 * 300 ) = 2.61 kg/m3
Mass flow rate of air,
m = ? A V
A = m / ? V
A = 0.25 / ( 2.61* 7.5 ) = 0.012 m2
As we know that area,
A = π D2 / 4
D= √((A*4)/π)
D= √((0.012*4)/3.14)
D = 0.127 m = 12.7 cm
A jet of water in upward direction is leave nozzle tip at the velocity of 15 m/s. The diameter of nozzle is 20 mm. suppose there is no energy loss during operation. What will be the diameter of water jet at 5 m above from the nozzle tip.
Ans.
First of all, imagine the system; the flow is in a vertical direction.
Data,
V1 = velocity of jet at the nozzle tip
V2 = velocity of jet at 5 m above from nozzle tip
Similarly, areas A1 and A2.
We have general equation of motion as below,
〖V2〗^2-〖V1〗^2=2 g s
〖V2〗^2-〖15〗^2=2*(-9.8)*5
V2 = 11.26 m/s
Now , apply continuity equation,
A1 V1 = A2 V2
A2 = (A1 V1)/ V2
A2= ((π/4)* (0.02)^2* 15)/11.26=4.18* 10^-4 m^2
π/4*〖d2〗^2 =4.18* 10^-4 m^2
Diameter = 0.023 m = 23 mm
Questions & Answers
What is the difference between the continuity equation and the Navier Stokes equation?
Fluids, by definition, can flow but it is fundamentally incompressible in nature. The continuity equation is a consequence of fact that what goes into a pipe/ hose must also release out. So, in the end, the area times the velocity at the end of a pipe/hose must remain constant.
In a necessary consequence if the area of the pipe/hose decreases, the fluid’s velocity must also increase to keep the flowrate constant.
While the Navier-Stokes equation describes the relations in between velocity, pressure, temperatures, and density of a moving fluid. This equation usually coupled with various differential equation forms. Usually, it’s pretty complex to solve analytically.
What is the continuity equation based on?
The equation of continuity says that the volume of fluid entering into the pipe of any cross-section should be equal to the volume of fluid leaving the other side of the cross-sectional area, which means the rate of flow rate should be constant and should follow the relation-
Suppose the fluid is incompressible (liquid), then the fluid density will not change at any point. It means that fluid density is constant.
A V = Constant
Flow rate = A1 V1 = A2 V2
What is the continuity equation used for?
Continuity equation has many applications in the field of Hydrodynamics, Aerodynamics, Electromagnetism, Quantum Mechanics. It is an important concept for the fundamental rule of Bernoulli’s Principle, it is indirectly involved in the Aerodynamics principle and applications.
The equation of continuity expresses a local conservation law depending on the context. It is merely a mathematical statement that is subtle yet very powerful concerning the local conservation of specific quantities.
Does the equation of continuity hold for supersonic flow?
Yes, It can be used for supersonic flow. It can be used for other flows like hypersonic, supersonic, and subsonic. The difference is that you have to use the conservative form of the equation.
What is the three-dimensional form of the continuity equation for steady incompressible flow?
If we consider flow is steady and incompressible. We know that in the case of steady flow ??/?t = 0. If the flow is incompressible, then density ? remains constant. So, by considering this condition, Eq. 8 can be written as,
∂u/∂x+ ∂v/∂y + ∂w/∂z =0
What is the 3D form of the continuity equation for steady compressible and incompressible flow?
In two-dimensional flow, there are two directions x and y. So, u velocity in x-direction and v velocity in the y-direction. There is no z-direction, so velocity in the z-direction is zero. By considering these conditions, the Eq. 8 turned as below,
∂/∂x (ρu)+ ∂/∂y (ρv)=0
∂u/∂x+ ∂v/∂y =0
Multiple Choice Questions
Which one of the following is a form of continuity equation?
- v1 A1 = v2 A2
- v1 t1 = v2 t2
- ΔV / t
- v1 / A1 = v2 / A2
What does the continuity equation give the concept about the movement of an ideal fluid?
- As the cross-sectional area increases, the speed increases.
- As the cross-sectional area decreases, the speed increases.
- As the cross-sectional area decreases, the speed decreases.
- As the cross-sectional area increases, the volume decreases.
- As the volume increases, the speed decreases.
The equation of continuity is based on the principle of
b) conservation of momentum
c) conservation of energy
d) conservation of force
Two similar pipe diameters of d converge to obtain a pipe of diameter D. What can be the observation between d and D?. The velocity of flow in the new pipe will be double that in each of the two pipes?
a) D = d
b) D = 2d
c) D = 3d
d) D = 4d
The pipes of different diameters d1 and d2 converge to obtain a pipe of diameter 2d. If the liquid velocity in both pipes is v1 and v2, what will be the flow velocity in the new pipe?
a) v1 + v2
b) v1 + v2/2
c) v1 + v2/4
d) 2(v1 + v2)
Conclusion
This article includes continuity equation derivations with their different form and conditions. Basic examples and questions are given for a better understanding of the concept of the continuity equation.
For more articles with related topics, click here
Read more Scientific Principles.

I am Deepak Kumar Jani, Pursuing PhD in Mechanical- Renewable energy. I have five years of teaching and two-year research experience. My subject area of interest are thermal engineering, automobile engineering, Mechanical measurement, Engineering Drawing, Fluid mechanics etc. I have filed a patent on “Hybridization of green energy for power production”. I have published 17 research papers and two books.
I am glad to be part of Lambdageeks and would like to present some of my expertise in a simplistic way with the readers.
Apart from academics and research, I like wandering in nature, capturing nature and creating awareness about nature among people.
Also refer my You-tube Channel regarding “Invitation from Nature”