A Comprehensive Guide to Calculating Lens Power

Calculating lens power is a crucial aspect of optical engineering and photography, as it determines the ability of a lens to distinguish between two lines or points in an object or scene. This comprehensive guide delves into the various methods and techniques used to measure and calculate lens power, providing a wealth of technical details and practical applications for physics students and enthusiasts.

Resolving Power of a Lens

Line Pairs per Millimeter (lp/mm)

The resolving power of a lens is measured in line pairs per millimeter (lp/mm), which represents the number of line pairs that can be distinguished within one millimeter of the image. This metric is essential in evaluating the quality and performance of a lens, as it directly impacts the level of detail and sharpness that can be captured.

To calculate the resolving power in lp/mm, the following formula can be used:

Resolving Power (lp/mm) = 1000 / (2 × Pixel Size (μm))

where the pixel size is measured in micrometers (μm). This theoretical calculation provides a baseline for the lens’s resolving power, which can then be verified through empirical testing.

Human Eye Perception Method

Another method for determining the resolving power of a lens involves the use of a resolution chart and the human eye’s perception. In this approach, the observer counts the number of line pairs in the chart until they become indistinguishable. The line width per picture height (LW/PH) value is then used to calculate the resolving power using the following formula:

Resolving Power (lp/mm) = 1000 / (2 × LW/PH)

This method takes into account the subjective nature of human visual perception and can provide a more practical assessment of the lens’s resolving power in real-world applications.

Theoretical Calculation

The resolving power of a lens can also be calculated theoretically using the following formula:

Image Space Resolution = 1000 / (2 × Pixel Size (μm))

This calculation is based on the Nyquist-Shannon sampling theorem, which states that the minimum sampling rate required to accurately represent a signal is twice the highest frequency present in the signal. By applying this principle to the image space, we can determine the theoretical resolving power of the lens.

Calculating Lens Power in Diopters

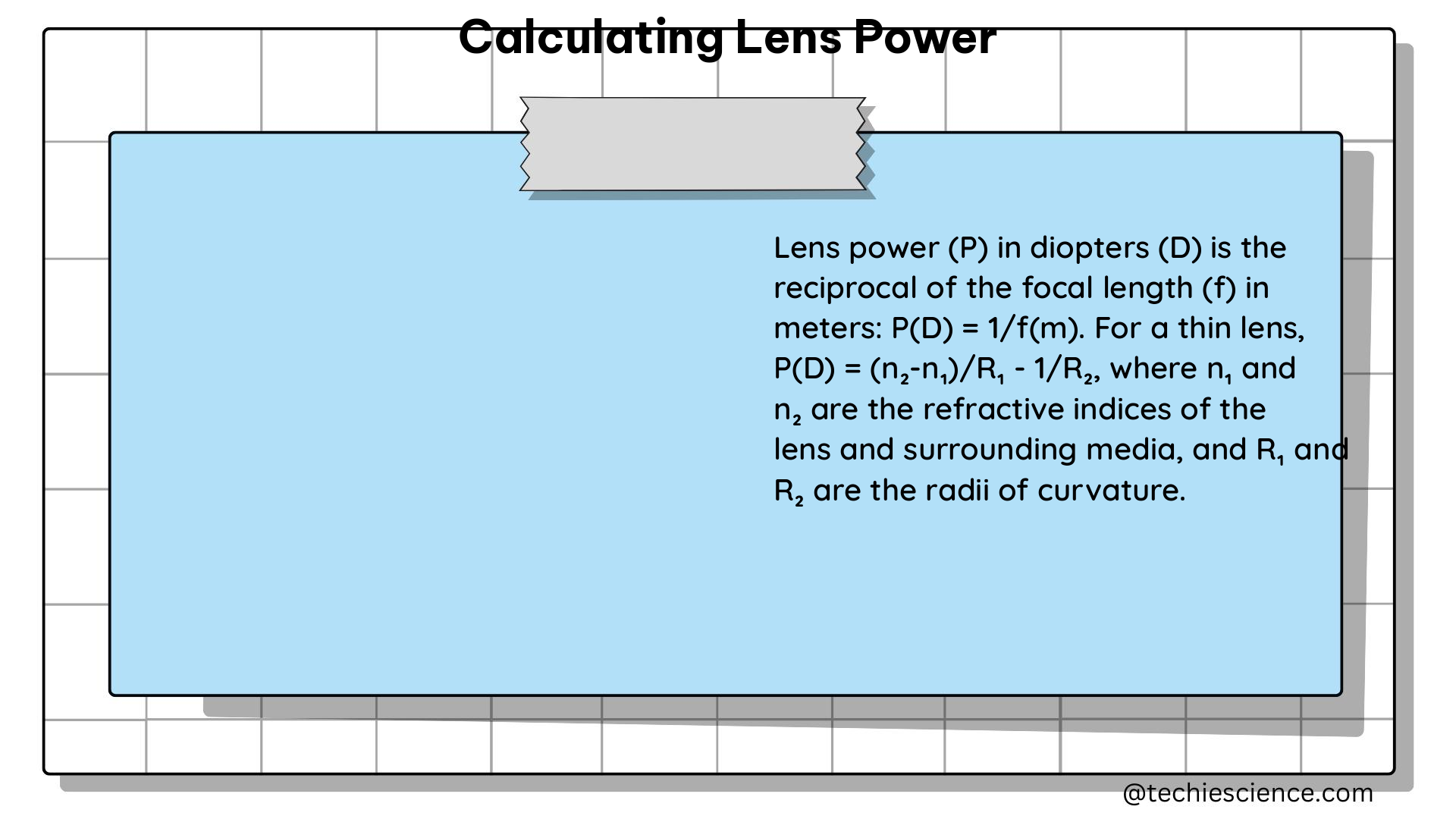
Power in Diopters

Lens power is commonly measured in diopters (D), which is the reciprocal of the focal length in meters. The formula for calculating lens power in diopters is:

Power in Diopters = 1 / Focal Length (m)

This means that lenses with shorter focal lengths have higher powers, as they can focus light more strongly. Conversely, lenses with longer focal lengths have lower powers and are better suited for capturing distant objects.

Calculating Crystalline Lens Power

Modification of the Bennett Method

The power of the crystalline lens, which is the natural lens inside the human eye, can be calculated using a modified version of the Bennett method. This approach combines extended depth OCT biometry, corneal topography, and refraction to measure the lens power. The formula for lens power is derived from a reduced eye model and involves ocular distances, corneal power, and objective spherical equivalent refraction.

Error Analysis

The modified Bennett method has a theoretical accuracy of ± 0.5 diopters (D) for refractive errors ranging from -10 D to +10 D. This level of precision is crucial in the field of ophthalmology, where accurate lens power calculations are essential for successful vision correction procedures and the design of intraocular lenses.

Practical Applications

Camera Lens Selection

Knowing the resolving power of a lens is crucial in choosing the right lens for a camera system. The resolving power directly affects the image quality, field of view, and depth of field, which are all important factors in capturing high-quality photographs. By understanding the resolving power of a lens, photographers can make informed decisions when selecting the appropriate lens for their specific needs.

Progressive Lens Design

The Camber Steady methodology provides a combination of objective and subjective measures to evaluate progressive lens designs. This approach includes the elimination of the “swim effect,” which is a common issue in progressive lenses, and the increased usable area for wider, undistorted fields of view. By considering the resolving power and other lens characteristics, designers can optimize the performance of progressive lenses to enhance the wearer’s experience.

References

1. e-con Systems. (2022). A Practical Guide to Calculating the Resolving Power of Your Camera Lens. Retrieved from https://www.e-consystems.com/blog/camera/technology/a-practical-guide-to-calculating-the-resolving-power-of-your-camera-lens/

2. ResearchGate. (2024). Calculation of Crystalline Lens Power Using a Modification of the Bennett Method. Retrieved from https://www.researchgate.net/publication/283276685_Calculation_of_crystalline_lens_power_using_a_modification_of_the_Bennett_method

3. 2020mag. (n.d.). Defining Success by the Wearer Experience–The Newly Patented Camber Steady Methodology. Retrieved from https://www.2020mag.com/article/defining-success-by-the-wearer-experiencethe-newly-patented-camber-steady-methodology

4. NCBI. (2015). Calculation of Crystalline Lens Power Using a Modification of the Bennett Method. Retrieved from https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4646557/

5. VAIA. (n.d.). Problem 36 What is the Power in Diopters of a Camera Lens? Retrieved from https://www.vaia.com/en-us/textbooks/physics/college-physics-1-edition/chapter-25/problem-36-what-is-the-power-in-diopters-of-a-camera-lens-th/