Butanol, a four-carbon alcohol with the molecular formula C4H9OH, is a versatile chemical compound with a wide range of applications in various industries. One of the critical physical properties of butanol is its density, which plays a crucial role in understanding its behavior and characteristics. This comprehensive guide delves into the intricacies of butanol density, providing a detailed exploration of the factors that influence it, the experimental data available, and the theoretical models used to predict its behavior.
Understanding Butanol Density: The Basics
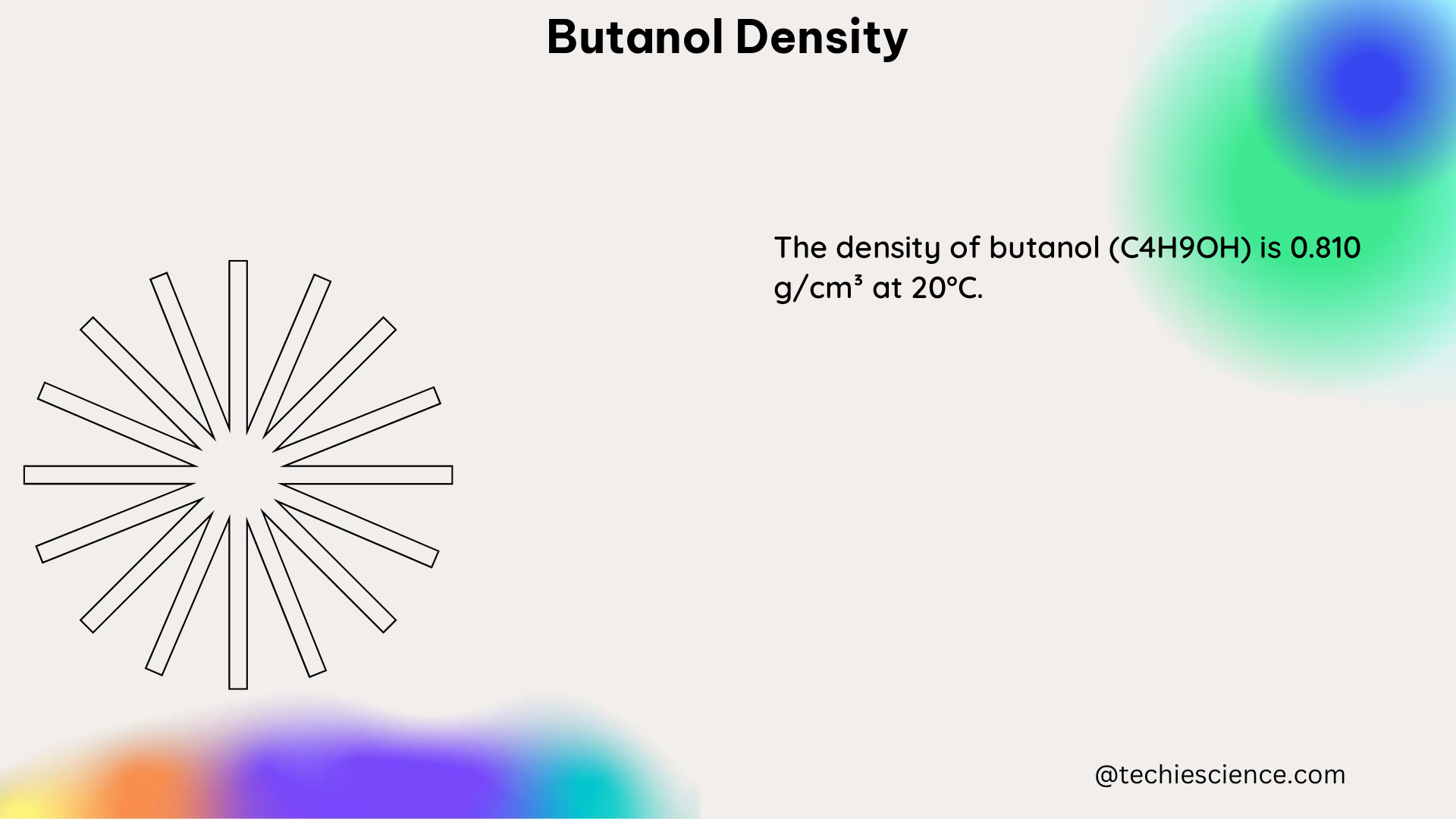
Butanol density, also known as the mass per unit volume of the substance, is a fundamental physical property that varies depending on temperature and pressure. At a standard temperature of 298.15 K (25°C) and atmospheric pressure (0.1 MPa), the density of 1-butanol is approximately 0.81 g/cm³. However, this value can change significantly under different conditions, as demonstrated by various experimental studies.
Experimental Data on Butanol Density
Numerous studies have been conducted to investigate the density of butanol under various temperature and pressure conditions. One such study, reported by Kiyohara and Tanaka (2011), provides a comprehensive dataset on the liquid density of 1-butanol at pressures up to 140 MPa and temperatures ranging from 293.15 K to 403.15 K.
The researchers used a vibrating-tube densimeter to measure the density of 1-butanol under these high-pressure and temperature conditions. The results of their study revealed that the density of 1-butanol increases with increasing pressure and decreases with increasing temperature. This relationship can be expressed mathematically using the following equation:
ρ = ρ₀ + (∂ρ/∂P)T × (P - P₀) - (∂ρ/∂T)P × (T - T₀)
Where:
– ρ is the density of 1-butanol at the given pressure (P) and temperature (T)
– ρ₀ is the density of 1-butanol at the reference pressure (P₀) and temperature (T₀)
– (∂ρ/∂P)T is the pressure derivative of the density at constant temperature
– (∂ρ/∂T)P is the temperature derivative of the density at constant pressure
By fitting the experimental data to this equation, the researchers were able to determine the values of the partial derivatives and accurately predict the density of 1-butanol at different temperatures and pressures.
Theoretical Models for Butanol Density Prediction
In addition to experimental data, researchers have also developed theoretical models to predict the density of butanol based on temperature and pressure. One such model is the Tait-like equation, which was used in a study by Alaoui et al. (2011) to fit the experimental density data for 1-butanol.
The Tait-like equation is a mathematical function that describes the relationship between the density, pressure, and temperature of a substance. The equation takes the following form:
ρ(T,P) = ρ(T,0) / [1 - C × ln(1 + P/B(T))]
Where:
– ρ(T,P) is the density of 1-butanol at temperature T and pressure P
– ρ(T,0) is the density of 1-butanol at temperature T and atmospheric pressure (0.1 MPa)
– C and B(T) are empirical parameters that are determined by fitting the experimental data
By fitting the experimental density data for 1-butanol to the Tait-like equation, the researchers were able to obtain the values of the empirical parameters C and B(T). These parameters can then be used to predict the density of 1-butanol at different temperatures and pressures with high accuracy.
Factors Affecting Butanol Density
In addition to temperature and pressure, the density of butanol can also be influenced by other factors, such as the presence of impurities or the crystallization of the substance. It is essential to specify the conditions under which the density is measured or predicted to ensure accuracy and consistency.
For example, the presence of water or other impurities in the butanol sample can affect its density. Similarly, the crystallization of butanol at low temperatures can also impact its density. Therefore, it is crucial to carefully control the experimental conditions and ensure the purity of the butanol sample when measuring or predicting its density.
Practical Applications of Butanol Density
The density of butanol is an important property that has numerous practical applications in various industries. For instance, in the chemical and petrochemical industries, the density of butanol is used to determine the volume and mass of the substance, which is crucial for storage, transportation, and processing.
Additionally, the density of butanol is a crucial parameter in the design and optimization of chemical processes, such as distillation, extraction, and reaction kinetics. Accurate knowledge of butanol density can help engineers and scientists to develop more efficient and cost-effective processes.
Furthermore, the density of butanol is also relevant in the biofuels industry, where it is considered as a potential alternative to traditional fossil fuels. The density of butanol can affect its combustion properties, energy content, and compatibility with existing fuel infrastructure, making it an important factor to consider in the development and implementation of butanol-based biofuels.
Conclusion
The density of butanol is a fundamental physical property that plays a crucial role in understanding the behavior and characteristics of this versatile chemical compound. This comprehensive guide has explored the experimental data, theoretical models, and factors that influence butanol density, providing a detailed and technical overview for physics students and professionals working in related fields.
By understanding the intricacies of butanol density, researchers and engineers can develop more accurate and efficient processes, optimize the use of this valuable chemical, and contribute to the advancement of various industries that rely on its unique properties.
References:
- Cheméo. (n.d.). Chemical Properties of 1-Butanol (CAS 71-36-3). Retrieved from https://www.chemeo.com/cid/45-788-8/1-Butanol
- Kiyohara, K., & Tanaka, T. (2011). Liquid density of 1-butanol at pressures up to 140 MPa and from 293.15 K to 403.15 K. Fluid Phase Equilibria, 307(1), 44-51.
- PubChem. (n.d.). 2-Butanol. Retrieved from https://pubchem.ncbi.nlm.nih.gov/compound/2-Butanol
- PubChem. (n.d.). 1-Butanol. Retrieved from https://pubchem.ncbi.nlm.nih.gov/compound/1-Butanol
- Alaoui, F., Montero, E., Bazile, J. P., Comuñas, M. J. P., Galliero, G., & Boned, C. (2011). Review Liquid density of 1-butanol at pressures up to 140 MPa and from 293.15 K to 403.15 K. Fluid Phase Equilibria, 307(1), 1-13.

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.