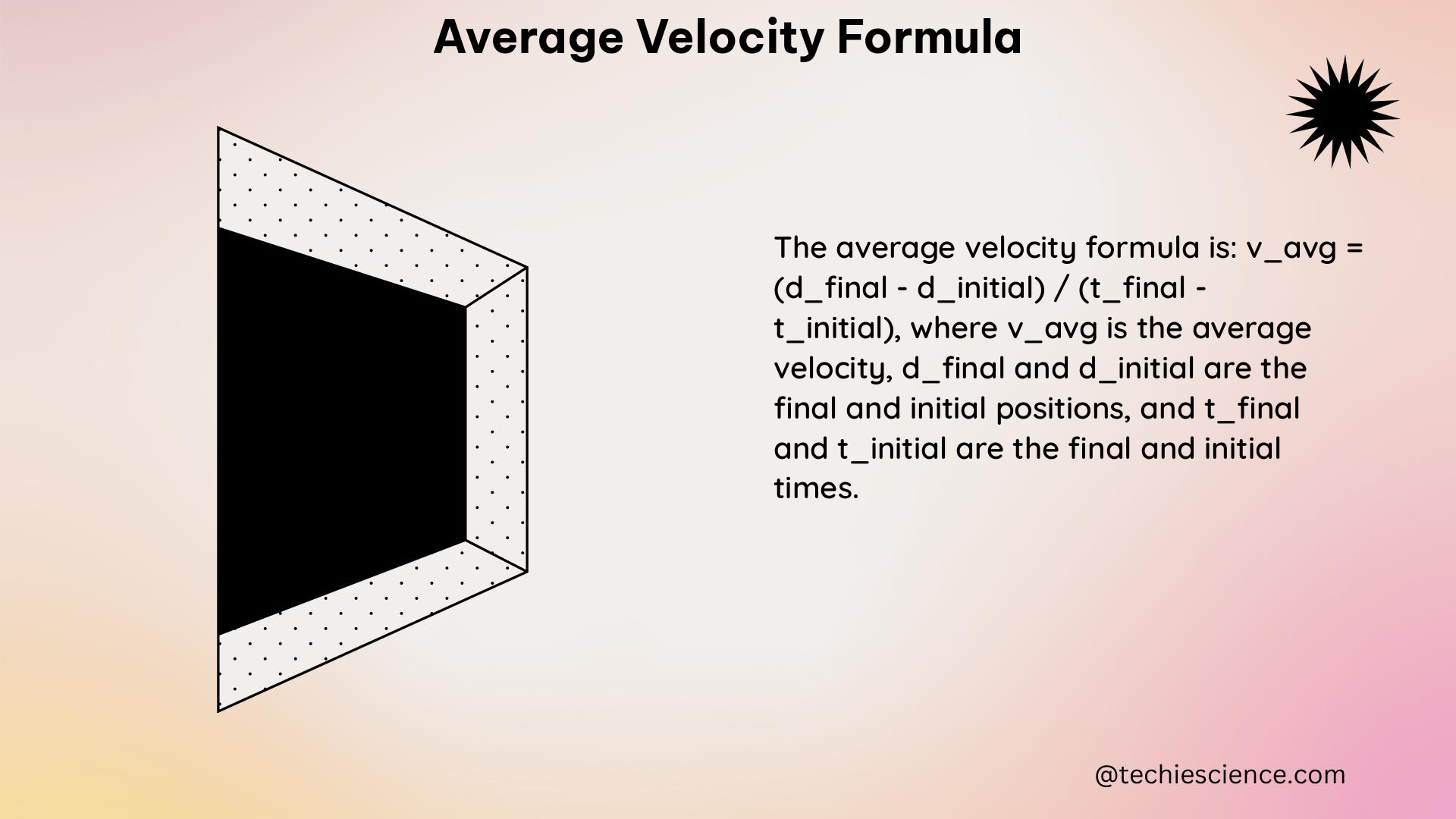
The average velocity formula is a fundamental concept in physics, particularly in the study of motion. It is used to calculate the average velocity of an object over a given period of time. The formula for average velocity is given by:
v_av = (s_1 + s_2 + ... + s_n) / (t_1 + t_2 + ... + t_n)
where v_av is the average velocity, s_1, s_2, …, s_n are the displacements of the object at different times t_1, t_2, …, t_n.
Understanding the Average Velocity Formula
The average velocity formula is derived from the definition of velocity, which is the displacement of an object divided by the time taken. The formula for average velocity is a simple arithmetic mean of the velocities at different instants of time.
The formula can be expressed as:
v_av = (Δs_1 + Δs_2 + ... + Δs_n) / (Δt_1 + Δt_2 + ... + Δt_n)
where Δs_i is the displacement of the object during the time interval Δt_i.
The unit of average velocity is the same as that of velocity, which is meters per second (m/s) in the International System of Units (SI).
Applications of the Average Velocity Formula
The average velocity formula is used in various branches of physics, including:
- Mechanics: Analyzing the motion of objects, such as cars, balls, and projectiles.
- Thermodynamics: Calculating the average speed of gas molecules in a system.
- Electromagnetism: Determining the average drift velocity of charge carriers in an electric field.
The average velocity formula is a useful tool for analyzing the motion of objects and predicting their future positions.
Examples of the Average Velocity Formula
Let’s explore some examples of how the average velocity formula is used in physics.
Example 1: Calculating the Average Velocity of a Car
A car travels a distance of 100 km in 2 hours. Calculate its average velocity.
Solution:
The average velocity of the car is given by:
v_av = (s_1 + s_2) / (t_1 + t_2)
where s_1 = s_2 = 100 km and t_1 = t_2 = 2 hours.
Substituting the values, we get:
v_av = (100 km + 100 km) / (2 hours + 2 hours)
v_av = 50 km/hour
Therefore, the average velocity of the car is 50 km/hour.
Example 2: Calculating the Average Velocity of a Vertically Thrown Ball
A ball is thrown vertically upward with an initial velocity of 20 m/s. Calculate its average velocity during the first 5 seconds of its motion.
Solution:
The ball reaches a maximum height and then falls back to the ground. The displacement of the ball during the first 5 seconds is not constant, but we can calculate its average velocity using the average velocity formula.
The initial velocity of the ball is 20 m/s, and its acceleration due to gravity is -9.8 m/s².
The displacement of the ball at time t is given by:
s = v_0 t + (1/2) a t²
where v_0 is the initial velocity and a is the acceleration due to gravity.
Substituting the values, we get:
s = 20 m/s × t + (1/2) (-9.8 m/s²) × t²
The average velocity of the ball during the first 5 seconds is given by:
v_av = (s_1 + s_2 + ... + s_5) / 5
where s_1, s_2, …, s_5 are the displacements of the ball at times t_1 = 1 s, t_2 = 2 s, …, t_5 = 5 s.
Substituting the values, we get:
v_av = [(20 m/s × 1 s - 4.9 m/s² × 1²) + (20 m/s × 2 s - 4.9 m/s² × 2²) + ... + (20 m/s × 5 s - 4.9 m/s² × 5²)] / 5
v_av = (175 m) / 5
v_av = 35 m/s
Therefore, the average velocity of the ball during the first 5 seconds of its motion is 35 m/s.
Additional Considerations
- Instantaneous Velocity vs. Average Velocity: The average velocity formula provides the average velocity over a given time interval, while instantaneous velocity is the velocity at a specific instant in time.
- Constant Velocity vs. Variable Velocity: If the velocity of an object is constant, the average velocity is equal to the instantaneous velocity. However, if the velocity is variable, the average velocity may differ from the instantaneous velocity.
- Displacement vs. Distance: The average velocity formula uses the displacement of the object, which is the change in position from the starting point to the ending point. This is different from the total distance traveled, which may be greater than the displacement.
- Negative Velocity: The average velocity formula can handle negative velocities, which may occur when an object is moving in the opposite direction.
- Multidimensional Motion: The average velocity formula can be extended to two-dimensional and three-dimensional motion by considering the displacements and time intervals in each dimension.
Conclusion
The average velocity formula is a fundamental concept in physics that is widely used to analyze the motion of objects. By understanding the formula, its derivation, and its applications, physics students can develop a deeper understanding of the principles of motion and use this knowledge to solve a variety of problems in various fields of physics.
References
- Average Velocity Formula – Derivation, Unit, Equation and FAQs. https://www.vedantu.com/jee-main/physics-average-velocity-formula
- Calculating average velocity or speed (video). https://www.khanacademy.org/science/physics/one-dimensional-motion/displacement-velocity-time/v/calculating-average-velocity-or-speed
- Average velocity – Nexus Wiki – ComPADRE. https://www.compadre.org/nexusph/course/Average_velocity
- Velocity in Scrum: How to Measure and Improve Performance. https://www.atlassian.com/agile/project-management/velocity-scrum

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.