Ankita Biswas - lambdageeks.com

11+ Dynamic Pressure Example:Detailed Facts

January 21, 2024April 15, 2022 by Ankita Biswas

In this article I’m going to explain what dynamic pressure is with 12+ dynamic pressure example.

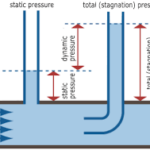
Dynamic pressure can be defined as the change in kinetic energy per unit mass of an incompressible fluid. The mathematical formula of Dynamic pressure is- Pd=1/2ᑭv^2 where ᑭ is the mass per unit volume and v is the velocity of the fluid.

12+ dynamic pressure example are written below:

Combustion Engine of a car
Turbomachines
Spacecrafts and Aircrafts
Oscillations
Processes related to Production
Robotics
Fluid Control processes
Pharmaceutical needs
Blast Waves
Ballistics
Automotive Industry
Frequency and Amplitude measurement

From Bernoulli’s theorem we can say that for an incompressible fluid the sum of change in pressure energy (p/ᑭ),kinetic energy(1/2v^2) and potential energy per unit mass(gh) is always constant. So the mathematical form of Bernoulli’s theorem is-

p/ᑭ+1/2v^2+gh=constant,where g is the gravitational acceleration. So here the second term of Bernoulli’s equation refers to the Dynamic Pressure(Pd) of a fluid. Normally mathematical expression of kinetic energy is 1/2.m.v^2. But here we have taken kinetic energy per unit mass that is why the expression has become 1/2v^2.

Mass(m)= volume(V) * density(ᑭ)

here,V=1 unit,

So, m=ᑭ and 1/2mv²= 1/2ᑭv^2=Pd

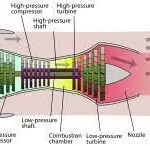
1.Combustion Engine of a car

Combustion engine of a car is one of the most important dynamic pressure example. Today the whole world is concerned about emissions of poisonous gasses from the combustion chamber of a car. So the measurement of dynamic pressure inside the gas cylinder of a car can make us able to detect whether the level of emission in a car is low or high.

2 1 — **Dynamic pressure measurement in a combustion engine from** wikipedia

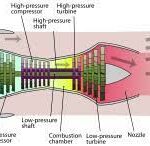
2. Turbomachines

Turbomachines are another important dynamic pressure example. Turbomachines are those machines which use blades to convert wind energy and mechanical energy into electrical or thermal energy. Examples of turbomachines are turbines,ceiling fans,exhaust fans,compressors etc. To measure the efficiencies of the turbomachines and to detect their sources of losses dynamic pressure measurement is necessary. To measure the value of thrust and to identify if the pressure is excess there dynamic pressure is measured in the rocket propulsion system.

3. Spacecrafts and Aircrafts

Construction and designing of spacecrafts and aircrafts need a stable structure to be used to fulfill human necessities. Unstable pressure within the spacecrafts and aircrafts can lead to complete destruction of them which in turn can cause deaths of many people. To avoid this problem dynamic pressure should be calculated accurately.

4 1 — **Spacecraft propulsion from** wikipedia

Sometimes this unstable pressure within the construction of vehicles and bridges can cause them to be damaged.

4. Oscillations

In acoustics mainly the oscillations that are low amplitude in nature measure the acoustic or sound pressure related to atmospheric pressure. This pressure is measured in decibel units. This pressure includes the noises within a house and outside the house,other external noises of vehicles,machinery of industrial areas etc.

The mathematical expression to calculate this oscillation pressure is

dB= 20 log(P/P0) where P is the gauge pressure and P0 is the atmospheric pressure here.

5. Processes related to Production

In the processes of plastic production, expulsion and die casting are done at a very high pressure but at very low frequency. So here in the production industry measurement or calculation of dynamic pressure is a much needed condition to extend the business and to increase both the quality and quantity of materials. It is another important dynamic pressure example to be noted.

6. Robotics

In today’s world robotics is moving at a very fast rate which will omit all human labor one day. In the body parts of robots we use pressure sensors to measure dynamic pressure. This in turn makes the robot work perfectly. These sensors usually act at a very low frequency. It is another notable dynamic pressure example.

7. Fluid Control processes

Machines based on hydraulic pressure like valves,pumps,engines,compressors etc help to control the movements of parts of objects. To know if these machines are acting perfectly the dynamic pressure should be calculated at a very high amplitude. Whenever a special activity is to be catched then a very high frequency should be maintained. It is one of the important dynamic pressure example.

Otherwise all operations within these machines require a low range of frequency. But in case of operations of pneumatic machines we require a low range of frequency and a low amplitude.

6 2 — **Dynamic pressure in fluids from** wikipedia

8. Pharmaceutical needs

In the blood pressure measurement of a patient there are two steady values of systolic and diastolic pressure. So the measurement of dynamic pressure gives us additional information about a patient’s health condition. Other than this orthopaedists use the method of walking of patients to measure their foot pressure which helps them to accurately identify the problem and to treat them properly.

In case of accidents or any other sudden health problem dynamic pressure measurement of body parts is also done in order to cure them.

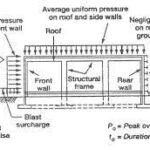
9. Blast Waves

When an explosive bursts it emits a pulse of pressure which is termed as blast wave. This can be an air blast or an underwater blast wave. Here the dynamic pressure measurement helps in two different ways. One is when the explosives need to test their maximum capability of destruction and the other is when the battalions want to check whether their shelters are able to stand firm against any kind of air blasts or not.

10. Ballistics

In the chamber of ballistic missiles,guns and other weapons,the value of dynamic pressure should be checked in order to resist any kind of explosions or other dangerous effects. This is another remarkable dynamic pressure example.

11. Automotive Industry

Exhaust pressure inside a vehicle is also measured. This is basically a parameter to control emissions from a vehicle. To achieve low emissions of hazardous gasses How much fuel should be injected in a cylinder of a vehicle to achieve low emissions of hazardous gasses is decided by this parameter.

12. Frequency and Amplitude measurement

Frequency and amplitude are heavily affected by the measurement of dynamic pressure in an instrument. Temperature range,fluid medium of which the dynamic pressure is being measured,chemical conditions etc also affect the value of dynamic pressure of a fluid. It is another notable dynamic pressure example.

Also, please click to know about 16+ Relative Pressure Example.

Also Read:

5 Absolute Pressure Example: Detailed Facts

January 21, 2024April 14, 2022 by Ankita Biswas

In this article I’m going to describe elaborately the definition and basics of absolute pressure equipped with absolute pressure example.

Whenever we feel the heavy flow of wind actually we feel the pressure of the air molecules. But there are no air molecules available in the space that is why pressure is absolutely zero in space. So the pressure which is measured above the absolute zero pressure of space or vacuum is known as Absolute pressure.

4+ absolute pressure example are given and described below:

Sensors that are based on the principle of Absolute pressure
Gauges that are based on the principle of Absolute pressure
Transmitters that are based on the principle of Absolute pressure
Transducers that are based on the principle of Absolute pressure
Pressure(P) at a point of a fluid is referred to as the normal force(F) exerted on that point of the fluid per unit area(A). P=F/A. In the case of a barometer the value of the pressure(P) depends upon the height(h) of the mercury level kept inside the barometer. The barometric pressure(P) can be calculated with the help of the following formula- P= pgh where p is the density of the mercury and g is the gravitational acceleration.Here the value of the absolute pressure( P absolute) is equivalent to the sum of atmospheric pressure(P atmospheric) and gauge pressure(P gauge).
P absolute= P atmospheric + P gauge

tabsolute pressure examplet — **Diagram of** **Absolute Pressure from** wikipedia

Sensors that are based on the principle of Absolute pressure

A sensor that acts on the principle of absolute pressure is a secured structure from which we can get readings of measurement of pressure that don’t include the effects of atmospheric pressure in them. Basically these sensors are semiconductor devices. There are wafers,N type semiconductors like silicon,polysilicon etc and piezoelectric materials available in the construction of pressure sensors.

**Manifold Absolute Pressure(MAP) sensor from** wikipedia

Combination of four resistors in the form of a wheatstone bridge is used here to cut the errors and to get a large output. In this type of sensor one of the edges that is out of contact of the pressure medium is revealed to a perfectly vacuum chamber which is closed forever and the other edge gets pressure from liquids or gasses. Piezoelectric effect is also produced here to get voltage that depends on absolute pressure. As this closed vacuum chamber is used as the absolute zero point by the diaphragm,the distortion of this never gets affected by the influence of the atmospheric pressure.

7 1 — **Sensors that are based on the principle of Absolute pressure** **from** wikipedia

These sensors are mainly used in the health industry and the food industry. In the health industry medicines and other medical products like injection syringes,scissors,knives that are used in operations should be sanitized and bacteria-free for the sake of safety of patients. So here packages should be air free which can be availed by using absolute pressure sensors. In the food industry foods also need vacuum packagings so that they can be preserved for a long time. These sensors which operate on the basis of absolute pressure mainly used to maintain an air free environment and resist the foods from being damaged.

Gauges that are based on the principle of Absolute pressure

Sometimes in the research laboratories where experiments based on weather conditions are being done, alteration of atmospheric pressure creates a huge problem to achieve the desired result. So here the gauges based on absolute pressure are used to make the experiment environment air free and vacuum in nature so that experimental readings should be perfect. These gauges are also used by aeronautics to avoid fluctuating atmospheric pressure and to get perfect measurement of altitudes. They also have uses in the food industry.

**Gauge based on absolute pressure from** wikipedia

**Digital pressure gauge from** wikipedia

Transmitters that are based on the principle of Absolute pressure

These kinds of transmitters are able to operate in vacuum. Pressure is measured by them in a completely air free environment. No external factors like changing weather conditions can influence them. In these transmitters the mechanical energy is converted into the electrical energy which in turn emits out in the form of electrical signals.

**Transmitter that acts on Absolute pressure** **from** wikipedia

Actually these types of transmitters are attached to the sensors which work on absolute pressure. The sensors used to send the outputs to the electrical unit where the absolute pressure is being calculated. After that this signal is transmitted through the transmitter. Transmitters related to absolute pressure are of two types- one is analog and the other is digital. The digital one converts the analog signal into digital.

In today’s world these types of transmitters are used to measure the altitudes,that is why these have wide usage in the navigation industry which has to deal with the directions and altitudes. Weather forecasting has become easier with the help of these modern transmitters that are based on the principle of Absolute pressure. There is no need for weather forecasting stations these days,pressure,temperature,humidity etc can be calculated through transmitters that are attached in computers,laptops and smartphones. These also have usage in the automation industry. They are used to measure the pressure of the engine of cars. They are also used in measuring depth of water of a well.

Transducers that are based on the principle of Absolute pressure

This kind of transducers contain a rigid tube,a flexible tube and a pipe wall. They are built on piezoelectric materials. They can measure dynamic as well as static pressure. These transducers usually convert the mechanical energy which is the applied pressure into the electrical energy in the form of signals. Every pressure transducer needs a supply voltage so that its internal circuit can work properly. Transducers that act on absolute pressure are usually a closed cavity that is placed inside an absolute sensor. These types of transducers help in detecting fluctuations of the barometric pressure.

5 1 — **Transducers** **that are based on the principle of Absolute pressure** **from** wikipedia

Also Read:

The Ratio of Rotational and Translational Kinetic Energy of a Sphere 2

June 25, 2024April 12, 2022 by Ankita Biswas

The ratio of the rotational kinetic energy to the translational kinetic energy of a sphere is a fundamental concept in classical mechanics. This ratio is an important parameter in understanding the dynamics of rolling motion and has various applications in fields such as engineering, sports, and robotics.

Understanding the Rotational and Translational Kinetic Energy of a Sphere

The rotational kinetic energy of a sphere is given by the formula:

$K_{rot} = \frac{1}{2}I\omega^2$

where $I$ is the moment of inertia and $\omega$ is the angular velocity of the sphere.

The moment of inertia of a sphere about its central axis is:

$I = \frac{2}{5}MR^2$

where $M$ is the mass of the sphere and $R$ is its radius.

The translational kinetic energy of the sphere is given by the formula:

$K_{trans} = \frac{1}{2}Mv^2$

where $v$ is the linear velocity of the center of mass of the sphere.

Calculating the Ratio of Rotational and Translational Kinetic Energy

To find the ratio of the rotational kinetic energy to the translational kinetic energy, we take the ratio of the two energies:

$\frac{K_{rot}}{K_{trans}} = \frac{\frac{1}{2}I\omega^2}{\frac{1}{2}Mv^2}$

Substituting the expressions for $I$ and $v$ (where $v = R\omega$), we get:

$\frac{K_{rot}}{K_{trans}} = \frac{\frac{1}{2}\left(\frac{2}{5}MR^2\right)\omega^2}{\frac{1}{2}M(R\omega)^2}$

Simplifying, we arrive at the final ratio:

$\frac{K_{rot}}{K_{trans}} = \frac{1}{5}$

This means that the translational kinetic energy of a sphere is five times greater than its rotational kinetic energy.

Technical Specifications and Importance

The moment of inertia of a sphere is a measure of its resistance to rotational motion. It has units of $kg\cdot m^2$ and is a crucial parameter in describing the rotational dynamics of a sphere.

The angular velocity of a sphere, $\omega$, is a measure of how fast it is rotating and has units of $rad/s$. It is related to the linear velocity $v$ through the equation $v = R\omega$.

Understanding the ratio of rotational and translational kinetic energy is important in various applications, such as:

Rolling Motion: The ratio of rotational to translational kinetic energy is crucial in understanding the dynamics of rolling motion, which is relevant in sports (e.g., bowling, golf) and industrial applications (e.g., wheel design, robotic locomotion).
Energy Efficiency: The ratio can be used to optimize the energy efficiency of systems involving rolling spheres, such as in the design of energy-efficient vehicles or machinery.
Stability and Control: The ratio of rotational to translational kinetic energy affects the stability and control of rolling objects, which is important in fields like robotics and aerospace engineering.
Collision Dynamics: The ratio of rotational to translational kinetic energy plays a role in the analysis of collisions involving rolling spheres, which is relevant in areas like sports, industrial processes, and particle physics.

Examples and Numerical Problems

Example 1: A solid sphere with a mass of 2 kg and a radius of 0.1 m is rolling on a horizontal surface with a linear velocity of 5 m/s. Calculate the ratio of its rotational kinetic energy to its translational kinetic energy.

Given:
– Mass of the sphere, $M = 2 kg$
– Radius of the sphere, $R = 0.1 m$
– Linear velocity of the sphere, $v = 5 m/s$

Step 1: Calculate the angular velocity of the sphere.
$\omega = \frac{v}{R} = \frac{5 m/s}{0.1 m} = 50 rad/s$

Step 2: Calculate the rotational kinetic energy of the sphere.
$K_{rot} = \frac{1}{2}I\omega^2 = \frac{1}{2}\left(\frac{2}{5}MR^2\right)(50 rad/s)^2 = 2.5 J$

Step 3: Calculate the translational kinetic energy of the sphere.
$K_{trans} = \frac{1}{2}Mv^2 = \frac{1}{2}(2 kg)(5 m/s)^2 = 25 J$

Step 4: Calculate the ratio of rotational to translational kinetic energy.
$\frac{K_{rot}}{K_{trans}} = \frac{2.5 J}{25 J} = \frac{1}{10}$

Example 2: A hollow sphere with a mass of 3 kg and an outer radius of 0.2 m is rolling on a horizontal surface with an angular velocity of 20 rad/s. Calculate the ratio of its rotational kinetic energy to its translational kinetic energy.

Given:
– Mass of the sphere, $M = 3 kg$
– Outer radius of the sphere, $R = 0.2 m$
– Angular velocity of the sphere, $\omega = 20 rad/s$

Step 1: Calculate the linear velocity of the sphere.
$v = R\omega = (0.2 m)(20 rad/s) = 4 m/s$

Step 2: Calculate the rotational kinetic energy of the sphere.
$K_{rot} = \frac{1}{2}I\omega^2 = \frac{1}{2}\left(\frac{2}{3}MR^2\right)(20 rad/s)^2 = 4 J$

Step 3: Calculate the translational kinetic energy of the sphere.
$K_{trans} = \frac{1}{2}Mv^2 = \frac{1}{2}(3 kg)(4 m/s)^2 = 24 J$

Step 4: Calculate the ratio of rotational to translational kinetic energy.
$\frac{K_{rot}}{K_{trans}} = \frac{4 J}{24 J} = \frac{1}{6}$

These examples demonstrate the application of the formulas and the calculation of the ratio of rotational to translational kinetic energy for both solid and hollow spheres.

Conclusion

The ratio of the rotational kinetic energy to the translational kinetic energy of a sphere is a fundamental concept in classical mechanics. This ratio is 1/5 for a solid sphere, meaning that the translational kinetic energy is five times greater than the rotational kinetic energy. Understanding this ratio is crucial in various applications, such as rolling motion, energy efficiency, stability and control, and collision dynamics. The moment of inertia and angular velocity are important technical specifications that contribute to the understanding of the rotational dynamics of a sphere.

References

Lumen Learning. “Moment of Inertia and Rotational Kinetic Energy.” Lumen Learning, https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/10-4-moment-of-inertia-and-rotational-kinetic-energy/.
YouTube. “If a sphere is rolling, the ratio of its rotational energy to the total kinetic energy is given by (1 …).” YouTube, https://www.youtube.com/watch?v=6HLPwSoCq_A.
YouTube. “If a sphere is rolling the ratio of the translational energy to … – YouTube.” YouTube, https://www.youtube.com/watch?v=1Ud5TyoNczM.
BYJU’S. “The ration of rotational to kinetic energy for a hollow sphere in pure rolling motio.” BYJU’S, https://byjus.com/question-answer/the-ration-of-rotational-to-kinetic-energy-for-a-hollow-sphere-in-pure-rolling-motio/.
Reddit. “Why does a sphere experience a larger translational kinetic energy … – Reddit.” Reddit, https://www.reddit.com/r/AskPhysics/comments/reyjlm/why_does_a_sphere_experience_a_larger/.

How to Find Conservation of Momentum: A Comprehensive Guide

June 25, 2024April 9, 2022 by Ankita Biswas

The conservation of momentum is a fundamental principle in physics that states the total momentum of a closed system remains constant unless acted upon by an external force. Mathematically, it is expressed as ptot = constant or ptot = p'tot (isolated system), where ptot is the initial total momentum and p'tot is the total momentum some time later.

Identifying the System

The first step in finding the conservation of momentum in a system is to identify the system under consideration. This involves ensuring that the system is a closed system, meaning that no external forces are acting on it. To do this, you should:

Clearly define the boundaries of the system, including all the objects or particles involved.
Ensure that there are no external forces acting on the system, such as gravity, friction, or applied forces.
Verify that the system is isolated, meaning that it does not exchange momentum with its surroundings.

Calculating Initial Momentum

Once the system has been identified, the next step is to calculate the initial total momentum (ptot) of the system. This is done by summing the momentum of all individual objects or particles within the system. The momentum of an object is given by the formula:

p = m * v

where p is the momentum, m is the mass, and v is the velocity of the object.

To calculate the initial total momentum, you would use the following equation:

ptot = p1 + p2 + p3 + ... + pn

where p1, p2, p3, …, pn are the momenta of the individual objects or particles in the system.

Calculating Final Momentum

After any interactions or collisions within the system, the final total momentum (p'tot) of the system must be calculated. This is done in the same way as the initial total momentum, but using the final velocities of the objects or particles:

p'tot = m1 * v1f + m2 * v2f + m3 * v3f + ... + mn * vnf

where v1f, v2f, v3f, …, vnf are the final velocities of the individual objects or particles.

Comparing Initial and Final Momentum

The final step in finding the conservation of momentum is to compare the initial total momentum (ptot) and the final total momentum (p'tot). If the system is closed and no external forces are acting on it, the total momentum should remain constant, meaning that ptot = p'tot.

If the initial and final momenta are equal, then the system is said to conserve momentum. If they are not equal, then the system does not conserve momentum, and there must be an external force acting on the system.

Theorem and Formulas

The conservation of momentum is a fundamental principle in physics, and it can be expressed mathematically as:

Theorem: In an isolated system, the total momentum is conserved.

Formulas:
– Initial total momentum: ptot = p1 + p2 + p3 + ... + pn
– Final total momentum: p'tot = m1 * v1f + m2 * v2f + m3 * v3f + ... + mn * vnf
– Conservation of momentum: ptot = p'tot

Examples and Numerical Problems

Example 1: Two objects with masses m1 = 2 kg and m2 = 3 kg are moving with initial velocities v1i = 4 m/s and v2i = -2 m/s, respectively. After a collision, the final velocities are v1f = 1 m/s and v2f = 1 m/s. Verify the conservation of momentum.

Solution:
1. Initial total momentum: ptot = m1 * v1i + m2 * v2i = 2 * 4 + 3 * (-2) = 8 - 6 = 2 kg·m/s
2. Final total momentum: p'tot = m1 * v1f + m2 * v2f = 2 * 1 + 3 * 1 = 2 + 3 = 5 kg·m/s
3. Comparing initial and final momentum: ptot = 2 kg·m/s and p'tot = 5 kg·m/s, so the system does not conserve momentum.

Numerical Problem 1: A 2 kg object is moving with an initial velocity of 5 m/s, and a 3 kg object is moving with an initial velocity of -3 m/s. After a collision, the final velocities are 2 m/s and -1 m/s, respectively. Verify the conservation of momentum.

Numerical Problem 2: Two objects with masses 4 kg and 6 kg are moving in opposite directions with initial velocities of 3 m/s and -2 m/s, respectively. After a perfectly elastic collision, the final velocities are 1 m/s and -1 m/s, respectively. Verify the conservation of momentum.

Figures and Data Points

To better illustrate the concept of conservation of momentum, consider the following figure:

In this figure, two objects with masses m1 and m2 are moving with initial velocities v1i and v2i, respectively. After a collision, the final velocities are v1f and v2f.

The data points for this example are:
– m1 = 2 kg
– m2 = 3 kg
– v1i = 4 m/s
– v2i = -2 m/s
– v1f = 1 m/s
– v2f = 1 m/s

Conclusion

In summary, to find the conservation of momentum in a system, you must:

Identify the system as a closed system with no external forces acting on it.
Calculate the initial total momentum (ptot) by summing the momenta of all individual objects or particles.
Calculate the final total momentum (p'tot) after any interactions or collisions, using the final velocities of the objects or particles.
Compare the initial and final momenta to determine if the system conserves momentum (ptot = p'tot).

By following these steps and applying the relevant formulas and theorems, you can accurately determine whether a system conserves momentum or not. This principle is fundamental in various fields of physics, from classical mechanics to quantum physics.

Reference:

http://hadron.physics.fsu.edu/~crede/TEACHING/PHY2053C/LAB-MANUALS/linearmomentum-1.pdf
https://courses.lumenlearning.com/suny-physics/chapter/8-3-conservation-of-momentum/
https://www.youtube.com/watch?v=SMebmMRS_2Q

A Comprehensive Guide on How to Find Perpendicular Vectors

June 25, 2024April 7, 2022 by Ankita Biswas

In the realm of linear algebra and vector mathematics, the ability to find vectors that are perpendicular to a given vector is a fundamental skill. Whether you’re a physics student, an engineer, or a mathematician, understanding the various methods and techniques for determining perpendicular vectors can be invaluable. This comprehensive guide will delve into the intricacies of finding perpendicular vectors, providing you with a thorough understanding of the subject matter.

Dot Product Method

The dot product, also known as the scalar product, is a powerful tool for determining whether two vectors are perpendicular. The dot product of two vectors A = (a1, a2, a3) and B = (b1, b2, b3) is defined as:

A ⋅ B = a1b1 + a2b2 + a3b3

If two vectors are perpendicular, their dot product is equal to zero. This means that if you have a vector U = (u1, u2, u3), you can find a vector V = (v1, v2, v3) that is perpendicular to U by solving the equation:

U ⋅ V = 0

For example, let’s say we have a vector U = (10, 4, -1). To find a vector V that is perpendicular to U, we can solve the equation:

U ⋅ V = 10v1 + 4v2 – v3 = 0

One possible solution is V = (v1, v2, -4v1 – 4v2), where v1 and v2 can be any real numbers.

Cross Product Method

The cross product, also known as the vector product, is another way to find a vector that is perpendicular to two given vectors. The cross product of two vectors A = (a1, a2, a3) and B = (b1, b2, b3) is defined as:

A × B = (a2b3 – a3b2, a3b1 – a1b3, a1b2 – a2b1)

The cross product of two non-parallel vectors results in a vector that is perpendicular to both of them.

For example, let’s say we have a vector U = (10, 4, -1). To find a vector V that is perpendicular to U, we can take the cross product of U and the unit vector X = (1, 0, 0):

U × X = (0, 1, 4)

The resulting vector (0, 1, 4) is perpendicular to U.

Gram-Schmidt Process

The Gram-Schmidt process is a method used in linear algebra to orthonormalize a set of linearly independent vectors. This process can be used to find a set of orthogonal vectors that span the same space as a given set of vectors.

Suppose you have a set of vectors U1, U2, and U3. You can use the Gram-Schmidt process to find a set of orthogonal vectors V1, V2, and V3 such that:

V1 is perpendicular to U2 and U3
V2 is perpendicular to U3
V3 is in the same space as U1, U2, and U3

The Gram-Schmidt process involves the following steps:

Choose the first vector U1 as the first orthogonal vector V1.
For each subsequent vector Ui, find the component of Ui that is perpendicular to the previous orthogonal vectors V1, V2, …, Vi-1, and use this component as the next orthogonal vector Vi.

By applying the Gram-Schmidt process, you can systematically construct a set of orthogonal vectors that span the same space as the original set of vectors.

Numerical Examples

Let’s consider some numerical examples to solidify our understanding of finding perpendicular vectors.

Example 1:
Given the vector U = (2, 3, -1), find a vector V that is perpendicular to U.

Using the dot product method, we can solve the equation U ⋅ V = 0 to find the components of V:

U ⋅ V = 2v1 + 3v2 – v3 = 0

One possible solution is V = (v1, v2, -2v1 – 3v2), where v1 and v2 can be any real numbers.

Example 2:
Given the vector U = (5, -2, 3), find a vector V that is perpendicular to U.

Using the cross product method, we can find a vector V that is perpendicular to U:

V = U × X = (0, 3, 2)

The vector V = (0, 3, 2) is perpendicular to U = (5, -2, 3).

Example 3:
Given the set of vectors U1 = (1, 2, 3), U2 = (2, -1, 1), and U3 = (3, 1, -2), find a set of orthogonal vectors V1, V2, and V3 using the Gram-Schmidt process.

Step 1: Choose V1 = U1 = (1, 2, 3).
Step 2: Find the component of U2 that is perpendicular to V1:
V2 = U2 – (U2 ⋅ V1 / V1 ⋅ V1) V1 = (2, -1, 1) – (1/14)(4, -2, 2) = (0, -1, -1).
Step 3: Find the component of U3 that is perpendicular to V1 and V2:
V3 = U3 – (U3 ⋅ V1 / V1 ⋅ V1) V1 – (U3 ⋅ V2 / V2 ⋅ V2) V2 = (3, 1, -2) – (3/14)(1, 2, 3) – (1/2)(0, -1, -1) = (2, 2, 0).

The set of orthogonal vectors is V1 = (1, 2, 3), V2 = (0, -1, -1), and V3 = (2, 2, 0).

These examples demonstrate the practical application of the dot product, cross product, and Gram-Schmidt process in finding perpendicular vectors. By understanding these methods, you can confidently tackle a wide range of problems involving the determination of perpendicular vectors.

Conclusion

In this comprehensive guide, we have explored the various methods and techniques for finding perpendicular vectors. From the dot product and cross product to the Gram-Schmidt process, you now have a solid understanding of the tools and strategies available to you. By mastering these concepts, you can effectively solve problems involving perpendicular vectors in physics, engineering, and mathematics.

Remember, the key to success in this domain is practice. Engage in a variety of exercises and problems to reinforce your understanding and develop your problem-solving skills. With dedication and persistence, you’ll become proficient in the art of finding perpendicular vectors.