A Comprehensive Guide to Understanding and Calculating Air Density

Air density is a crucial concept in physics and engineering, as it represents the mass per unit volume of Earth’s atmosphere. This parameter is essential in various applications, from aerodynamics and meteorology to environmental studies and engineering design. Understanding the factors that influence air density and the methods to calculate it accurately is crucial for many scientific and technological endeavors.

Defining Air Density

Air density, denoted by the Greek letter ρ (rho), is the mass of air per unit volume. It is typically measured in kilograms per cubic meter (kg/m³) or pounds per cubic foot (lb/ft³). The density of air can vary significantly depending on factors such as atmospheric pressure, temperature, and humidity.

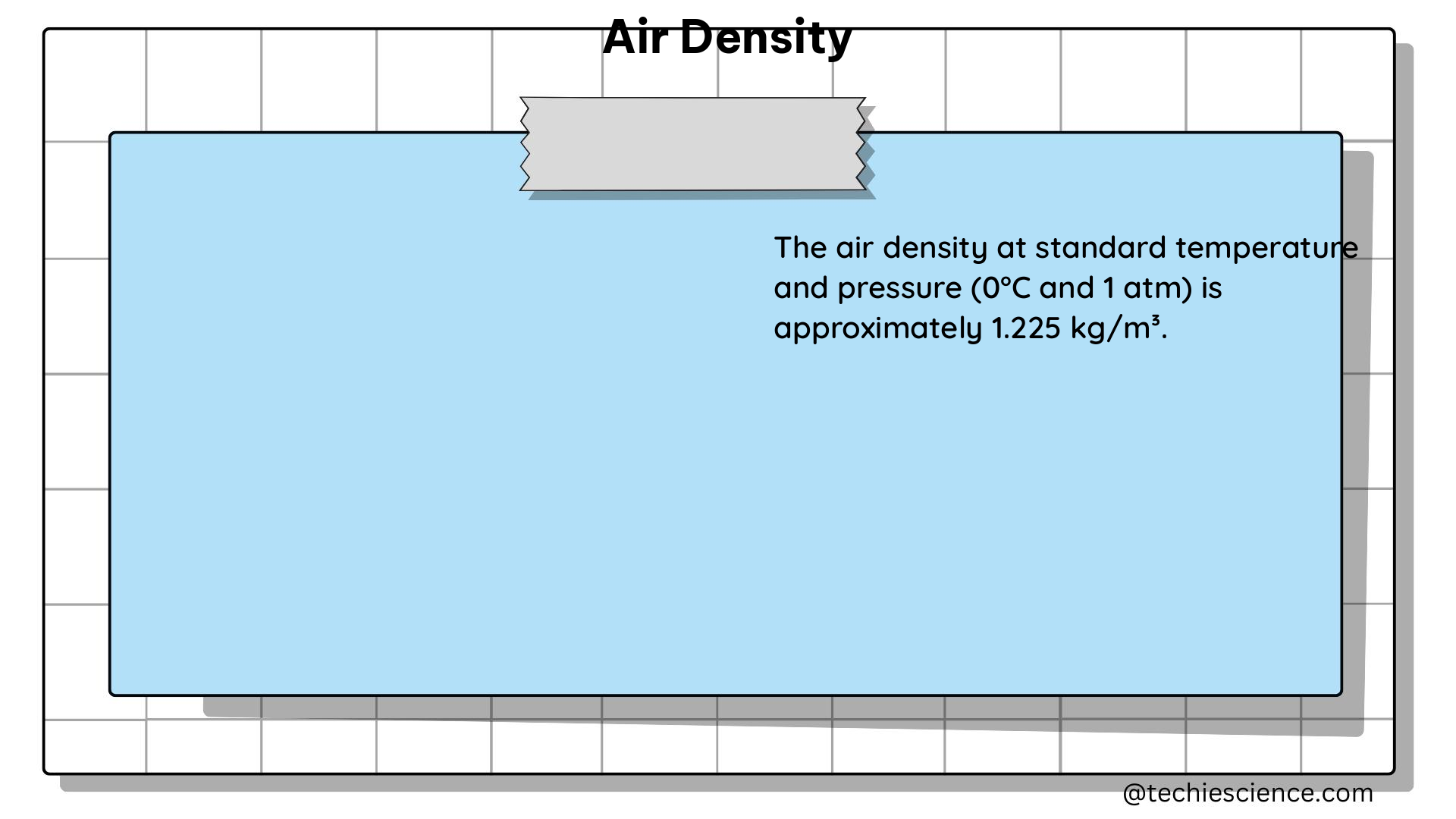
At standard conditions, defined as 101.325 kPa (abs) and 20 °C (68 °F), the air density is approximately 1.204 kg/m³ (0.0752 lb/ft³), according to the International Standard Atmosphere (ISA).

Factors Affecting Air Density

The density of air is influenced by several environmental variables, including:

1. Atmospheric Pressure: As altitude increases, the atmospheric pressure decreases, leading to a lower air density.
2. Temperature: Higher temperatures result in lower air density, as the air molecules have more kinetic energy and occupy a larger volume.
3. Humidity: The presence of water vapor in the air reduces the overall air density, as water vapor has a lower molar mass compared to dry air.

Calculating Air Density

To calculate the air density as a function of altitude, we can use the following formula, which is valid for the troposphere (the lowest part of the atmosphere, up to approximately 10 km):

ρ = (p₀M) / (RT₀) × (1 – Lh/T₀)^((gM/RL) – 1)

Where:
– ρ is the air density (kg/m³)
– p₀ is the sea-level standard atmospheric pressure (101,325 Pa)
– M is the molar mass of dry air (0.0289652 kg/mol)
– R is the universal gas constant (8.31446 J/(mol·K))
– T₀ is the sea-level standard temperature (288.15 K)
– L is the temperature lapse rate (0.0065 K/m)
– h is the altitude above sea level (m)
– g is the Earth’s surface gravitational acceleration (9.80665 m/s²)

This formula takes into account the changes in temperature and pressure with altitude, allowing for the calculation of air density at different elevations.

Example Calculation

Let’s calculate the air density at an altitude of 2,000 meters (6,562 feet) above sea level.

Given:
– p₀ = 101,325 Pa
– T₀ = 288.15 K
– L = 0.0065 K/m
– h = 2,000 m
– M = 0.0289652 kg/mol
– R = 8.31446 J/(mol·K)
– g = 9.80665 m/s²

Substituting the values into the formula:
T = T₀ – Lh = 288.15 K – (0.0065 K/m × 2,000 m) = 273.15 K
p = p₀ × (1 – Lh/T₀)^(gM/RL) = 101,325 Pa × (1 – 0.0065 × 2,000 / 288.15)^(9.80665 × 0.0289652 / (8.31446 × 0.0065)) = 79,502 Pa
ρ = (p₀M) / (RT₀) × (1 – Lh/T₀)^((gM/RL) – 1) = (101,325 × 0.0289652) / (8.31446 × 288.15) × (1 – 0.0065 × 2,000 / 288.15)^((9.80665 × 0.0289652 / (8.31446 × 0.0065)) – 1) = 0.955 kg/m³

Therefore, the air density at an altitude of 2,000 meters is approximately 0.955 kg/m³.

Uncertainties in Air Density Calculations

It’s important to note that the accuracy of air density calculations depends on the precision and accuracy of the input parameters, such as atmospheric pressure, temperature, and humidity. Uncertainties in these measurements can lead to significant errors in the final air density value.

To minimize these uncertainties, it is crucial to use high-quality instruments and follow proper measurement protocols. Additionally, the air density equation assumes that the air is dry and behaves as an ideal gas, which may not always be the case, especially in humid environments.

Applications of Air Density

Air density is a critical parameter in various fields, including:

1. Aerodynamics: Air density is a key factor in determining the lift and drag forces acting on aircraft, vehicles, and other objects moving through the air.
2. Meteorology: Air density is used in weather forecasting models to predict atmospheric conditions, such as wind patterns and air pressure.
3. Environmental Studies: Air density is important in understanding the transport and dispersion of air pollutants, as well as the behavior of atmospheric gases.
4. Engineering Design: Air density is considered in the design of structures, such as buildings and bridges, to ensure they can withstand wind loads.
5. Sports and Recreation: Air density affects the performance of sports equipment, such as golf balls and baseballs, as well as the flight of projectiles.

Conclusion

Air density is a fundamental concept in physics and engineering, with far-reaching applications. Understanding the factors that influence air density and the methods to calculate it accurately is crucial for a wide range of scientific and technological endeavors. By mastering the principles and techniques presented in this guide, you can become proficient in understanding and applying air density in your own work.

References

1. Measuring air density – where is my huge error coming from? (2016-10-21). Retrieved from https://physics.stackexchange.com/questions/287877/measuring-air-density-where-is-my-huge-error-coming-from
2. How to Calculate Air Density | Sciencing (2023-03-12). Retrieved from https://sciencing.com/calculate-air-density-5149935.html
3. Density of air – Wikipedia. Retrieved from https://en.wikipedia.org/wiki/Density_of_air
4. The Air Density Equation and the Transfer of the Mass Unit – NCBI (n.d.). Retrieved from https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6764509/