Calculating Elastic Energy in Archery Bows: A Comprehensive Guide

Archery bows are remarkable examples of engineering, harnessing the principles of elasticity to propel arrows with tremendous force. Understanding the calculation of elastic energy in these bows is crucial for archers, engineers, and physics enthusiasts alike. In this comprehensive guide, we will delve into the intricacies of this process, providing a step-by-step approach to accurately determine the elastic energy stored in archery bows.

Hooke’s Law and the Work Done in Pulling the String

The foundation of calculating elastic energy in archery bows lies in Hooke’s law, which states that the force required to stretch or compress a spring is proportional to the distance of the displacement. In the case of a bow, the string acts as a spring, and the force needed to pull it back increases linearly with the distance.

The work done in pulling the string back can be calculated using the formula for work, which is the integral of the force over the distance:

Work = ∫ F(x) dx

Where F(x) is the force required to pull the string back a distance x.

Assuming the bow follows Hooke’s law, the force F(x) can be expressed as:

F(x) = k * x

Where k is the spring constant of the bow, and x is the distance the string is pulled back.

Substituting this into the work formula, we get:

Work = ∫ k * x dx = (1/2) * k * x^2

This represents the work done in pulling the string back a distance x.

Calculating the Elastic Potential Energy Stored in the Bow

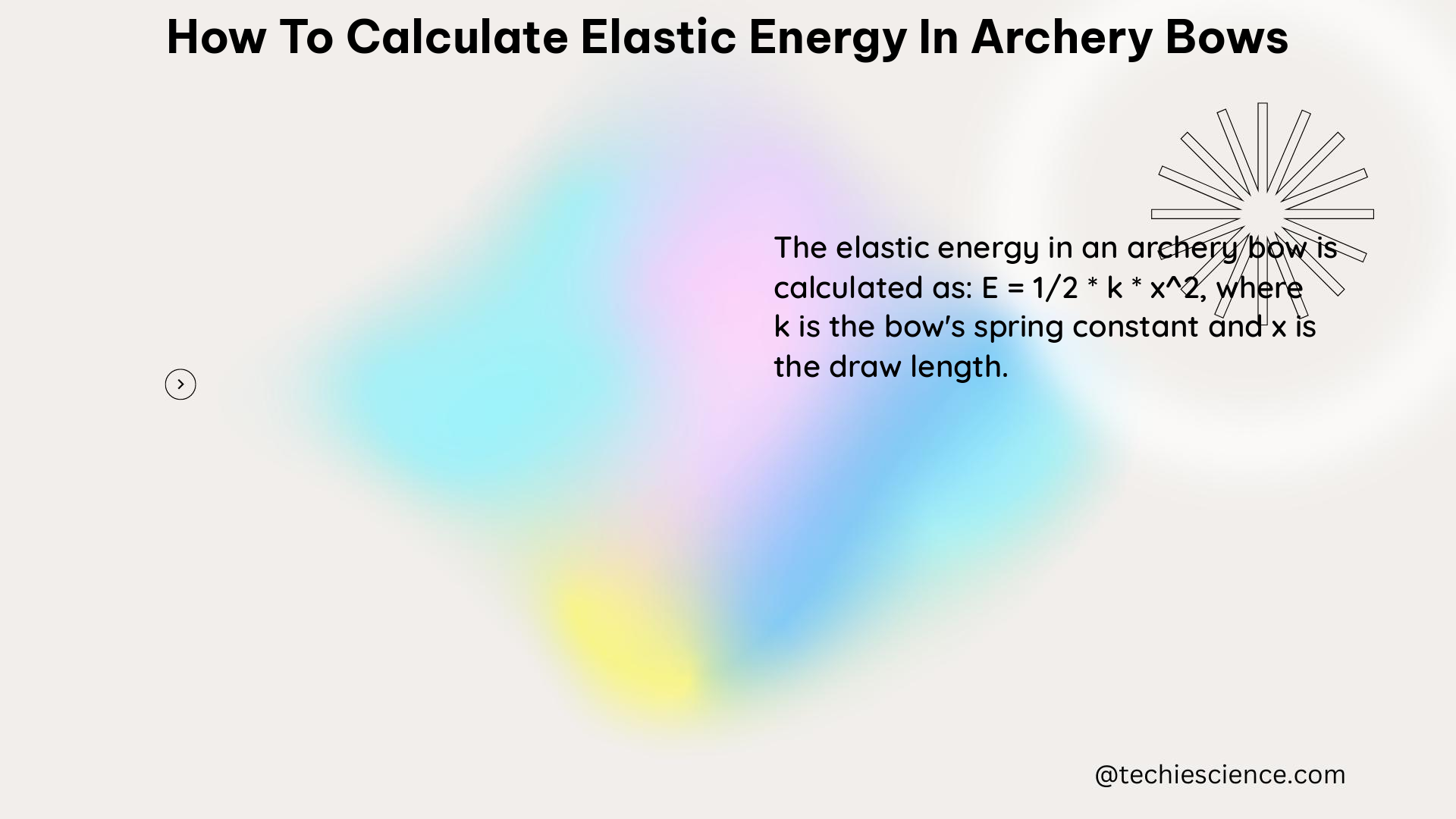
The elastic potential energy stored in the bow can be calculated using the formula for elastic potential energy:

Elastic Potential Energy = (1/2) * k * x^2

Where k is the spring constant of the bow, and x is the distance the string is pulled back.

For example, if the spring constant of the bow is 272 N/m and the string is pulled back 10 cm (0.1 m), the elastic potential energy stored in the bow would be:

Elastic Potential Energy = (1/2) * 272 N/m * (0.1 m)^2 = 1.36 J

Energy Losses and Efficiency

It’s important to note that not all of the elastic potential energy stored in the bow is transferred to the arrow. Some energy is lost due to various factors, such as:

1. Internal Friction in the Limbs: As the bow is drawn, the limbs flex and rub against each other, causing energy dissipation.
2. Mechanical Friction in the Cams: In compound bows, the cams and pulleys can introduce mechanical friction, leading to energy losses.
3. Vibrations and Noise: When the bow is released, some energy is lost in the form of vibrations and noise.

In traditional wooden bows, these energy losses can account for up to 20% of the total energy stored in the bow. In modern compound bows, the efficiency can be as high as 80-90%, with only 10-20% of the energy lost.

Calculating the Kinetic Energy of the Arrow

To determine the kinetic energy of the arrow, we need to consider the mass of the arrow and its final velocity. The formula for kinetic energy is:

Kinetic Energy = (1/2) * m * v^2

Where m is the mass of the arrow, and v is the final velocity of the arrow.

For example, if the mass of the arrow is 34.3 grams (0.0343 kg) and the final velocity of the arrow is 30 m/s, the kinetic energy of the arrow would be:

Kinetic Energy = (1/2) * 0.0343 kg * (30 m/s)^2 = 4.41 J

Numerical Examples and Calculations

Let’s consider a few numerical examples to illustrate the calculations involved in determining the elastic energy in archery bows.

Example 1:
* Bow spring constant (k): 272 N/m
* Draw length (x): 0.1 m (10 cm)

1. Work done in pulling the string back:
   Work = (1/2) * k * x^2
   Work = (1/2) * 272 N/m * (0.1 m)^2
   Work = 1.36 J

2. Elastic potential energy stored in the bow:
   Elastic Potential Energy = (1/2) * k * x^2
   Elastic Potential Energy = (1/2) * 272 N/m * (0.1 m)^2
   Elastic Potential Energy = 1.36 J

Example 2:
* Bow spring constant (k): 350 N/m
* Draw length (x): 0.15 m (15 cm)

1. Work done in pulling the string back:
   Work = (1/2) * k * x^2
   Work = (1/2) * 350 N/m * (0.15 m)^2
   Work = 3.94 J

2. Elastic potential energy stored in the bow:
   Elastic Potential Energy = (1/2) * k * x^2
   Elastic Potential Energy = (1/2) * 350 N/m * (0.15 m)^2
   Elastic Potential Energy = 3.94 J

Example 3:
* Arrow mass (m): 0.0343 kg (34.3 grams)
* Arrow final velocity (v): 30 m/s

1. Kinetic energy of the arrow:
   Kinetic Energy = (1/2) * m * v^2
   Kinetic Energy = (1/2) * 0.0343 kg * (30 m/s)^2
   Kinetic Energy = 4.41 J

These examples demonstrate the step-by-step process of calculating the elastic energy in archery bows, considering the work done, the stored elastic potential energy, and the resulting kinetic energy of the arrow.

Conclusion

Calculating the elastic energy in archery bows is a crucial aspect of understanding the physics behind these remarkable devices. By applying the principles of Hooke’s law, work, and kinetic energy, we can accurately determine the energy stored in the bow and the energy transferred to the arrow. This knowledge is valuable for archers, engineers, and anyone interested in the science behind archery.

Remember, the key factors in these calculations are the bow’s spring constant, the draw length, the arrow’s mass, and the arrow’s final velocity. By mastering these concepts, you can gain a deeper appreciation for the engineering and physics behind the art of archery.

References

1. Wired: How Much Energy from a Bow Goes into the Kinetic Energy of the Arrow?
2. Outlab: The Physics of Archery
3. arXiv: The Physics of Archery
4. Bowhunting.com: How Much Kinetic Energy for Bowhunting?
5. Harvard University: The Bow and Arrow