How to Find Acceleration Vector: A Comprehensive Guide

Acceleration is a fundamental concept in physics, and understanding how to find the acceleration vector is crucial for analyzing the motion of objects. This comprehensive guide will walk you through the step-by-step process of determining the acceleration vector, including the necessary formulas, examples, and practical applications.

Understanding Acceleration as a Vector Quantity

Acceleration is a vector quantity, meaning it has both magnitude and direction. To fully describe the acceleration of an object, we need to know both its magnitude (the rate of change in velocity) and its direction (the orientation of the acceleration vector).

The acceleration vector can be represented by the symbol a, and it is typically expressed in terms of its components along the x and y axes, denoted as a_x and a_y, respectively.

Step 1: Identify the Given Values

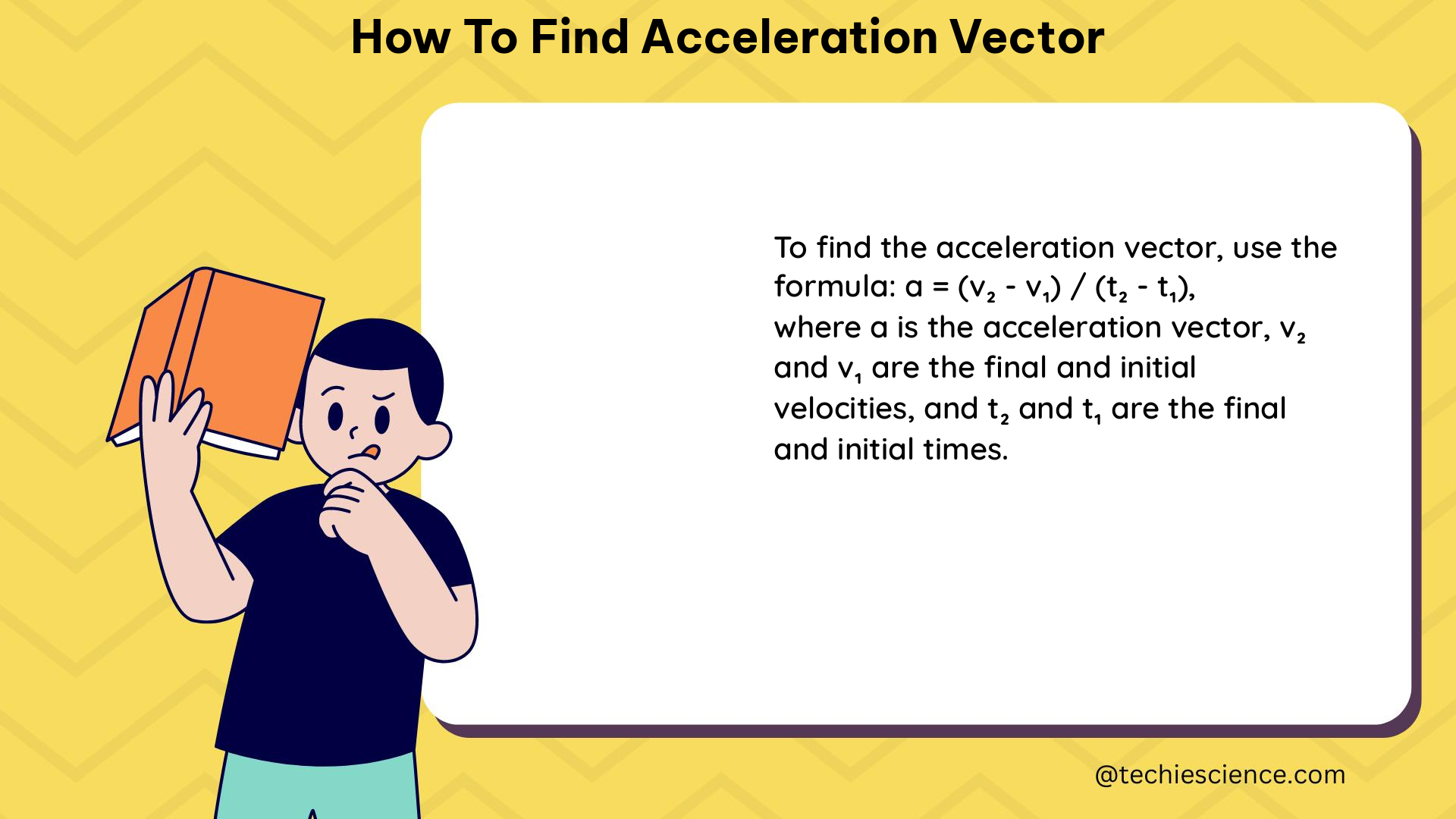
The first step in finding the acceleration vector is to identify the given values of acceleration (a) and its direction (θ) with reference to the horizontal direction (x-axis). This information is crucial for determining the components of the acceleration vector.

Step 2: Use the Acceleration Vector Formulas

Once you have the magnitude and direction of the acceleration, you can use the following formulas to find the x and y components of the acceleration vector:

1. X-component (Horizontal): a_x = a cos(θ)
2. Y-component (Vertical): a_y = a sin(θ)

Where:
– a_x and a_y represent the x and y components of the acceleration vector, respectively.
– a is the magnitude of the acceleration.
– θ is the angle made by the acceleration vector with the positive x-axis.

Step 3: Plug in the Values

After identifying the values of a and θ, you can substitute them into the formulas to find the components of the acceleration vector.

Step 4: Calculate the Acceleration Vector Components

Once you have the values of a_x and a_y, you can calculate the acceleration vector by combining its components. The magnitude of the acceleration vector is given by:

Magnitude of the Acceleration Vector: √(a_x^2 + a_y^2)

And the direction of the acceleration vector is given by:

Direction of the Acceleration Vector: tan^(-1)(a_y/a_x)

Remember to include the appropriate units for each component of the acceleration vector.

Example: Finding the Acceleration Vector of a Car in Circular Motion

Let’s consider an example to illustrate the process of finding the acceleration vector.

Suppose a car is moving in a circular path with a constant speed of 20 m/s and a radius of 100 m. Find the acceleration vector of the car at a particular instant when its direction is towards the north.

Solution:

1. We know the speed of the car is constant, and its direction is towards the north. Therefore, the acceleration vector of the car is always towards the center of the circular path, which is perpendicular to the direction of motion.
2. The magnitude of the acceleration vector is given by the formula: a = v^2/r, where v is the speed of the car and r is the radius of the circular path. Substituting the given values, we get a = (20 m/s)^2 / 100 m = 4 m/s^2.
3. Since the direction of the acceleration vector is towards the center of the circular path, which is perpendicular to the north direction, we can resolve the acceleration vector into its horizontal and vertical components.
4. Using the formulas a_x = a cos(θ) and a_y = a sin(θ), we can find the horizontal and vertical components of the acceleration vector. Here, θ is the angle made by the acceleration vector with the positive x-axis. Since the direction of the acceleration vector is towards the center of the circular path, which is at an angle of 90 degrees with the positive x-axis, we have θ = 90 degrees.
5. Substituting the values, we get a_x = 4 m/s^2 * cos(90 degrees) = 0, and a_y = 4 m/s^2 * sin(90 degrees) = 4 m/s^2.
6. Therefore, the acceleration vector of the car at the particular instant is (0, 4) m/s^2, which has a magnitude of 4 m/s^2 and is directed towards the center of the circular path.

Additional Considerations and Applications

• The acceleration vector can be used to analyze the motion of objects in various scenarios, such as projectile motion, circular motion, and uniform acceleration.
• In addition to the formulas presented, there are other methods and techniques for finding the acceleration vector, such as using vector addition or the derivative of the velocity vector.
• The acceleration vector is a crucial concept in the study of dynamics, as it is directly related to the net force acting on an object through Newton’s second law of motion.
• Understanding the acceleration vector is also important in the design and analysis of various engineering systems, such as vehicles, robots, and aerospace applications.

Conclusion

Mastering the skill of finding the acceleration vector is essential for a deep understanding of physics and its practical applications. By following the step-by-step process outlined in this guide, you can confidently determine the acceleration vector of an object, whether it’s in linear, circular, or any other type of motion. Remember to practice with various examples and numerical problems to solidify your understanding of this fundamental concept.

References

1. Physics LibreTexts. (2022). 4.3: Acceleration Vector. Retrieved from https://phys.libretexts.org/Bookshelves/University_Physics/University_Physics_%28OpenStax%29/Book:_University_Physics_I_-_Mechanics_Sound_Oscillations_and_Waves_%28OpenStax%29/04:_Motion_in_Two_and_Three_Dimensions/4.03:_Acceleration_Vector
2. The College Board. (2015). AP Physics 1 Investigation 2: Newton’s Second Law. Retrieved from https://www.paulding.k12.ga.us/cms/lib010/GA01903603/Centricity/Domain/525/ap%20physics%201investigation2newtonssecondlaw.pdf
3. Talkboard. (2014). Acceleration Vectors Example. Retrieved from https://www.youtube.com/watch?v=XSWrSfK2x4c