Gravity on a slope is a fundamental concept in physics that describes the behavior of objects under the influence of gravity on an inclined surface. This comprehensive guide will delve into the intricacies of this topic, providing a detailed exploration of the underlying principles, formulas, and practical applications.
Galileo’s Inclined Plane Experiment
The foundation of understanding gravity on a slope lies in Galileo’s Inclined Plane Experiment. Galileo designed this experiment to accurately measure the effect of gravity on free-falling bodies by using an inclined plane to slow down the acceleration of a ball, making it easier to observe and measure the phenomenon.
The Acceleration Due to Gravity (g)
The formula for calculating the acceleration due to gravity (g) is:
g = (d²)/(2s)
where:
– g is the acceleration due to gravity
– d is the distance traveled by the ball
– s is the time taken to travel the distance
This formula allows us to determine the acceleration due to gravity on a level surface, which is a crucial parameter in understanding gravity on a slope.
Acceleration Due to Gravity on a Slope (g’)
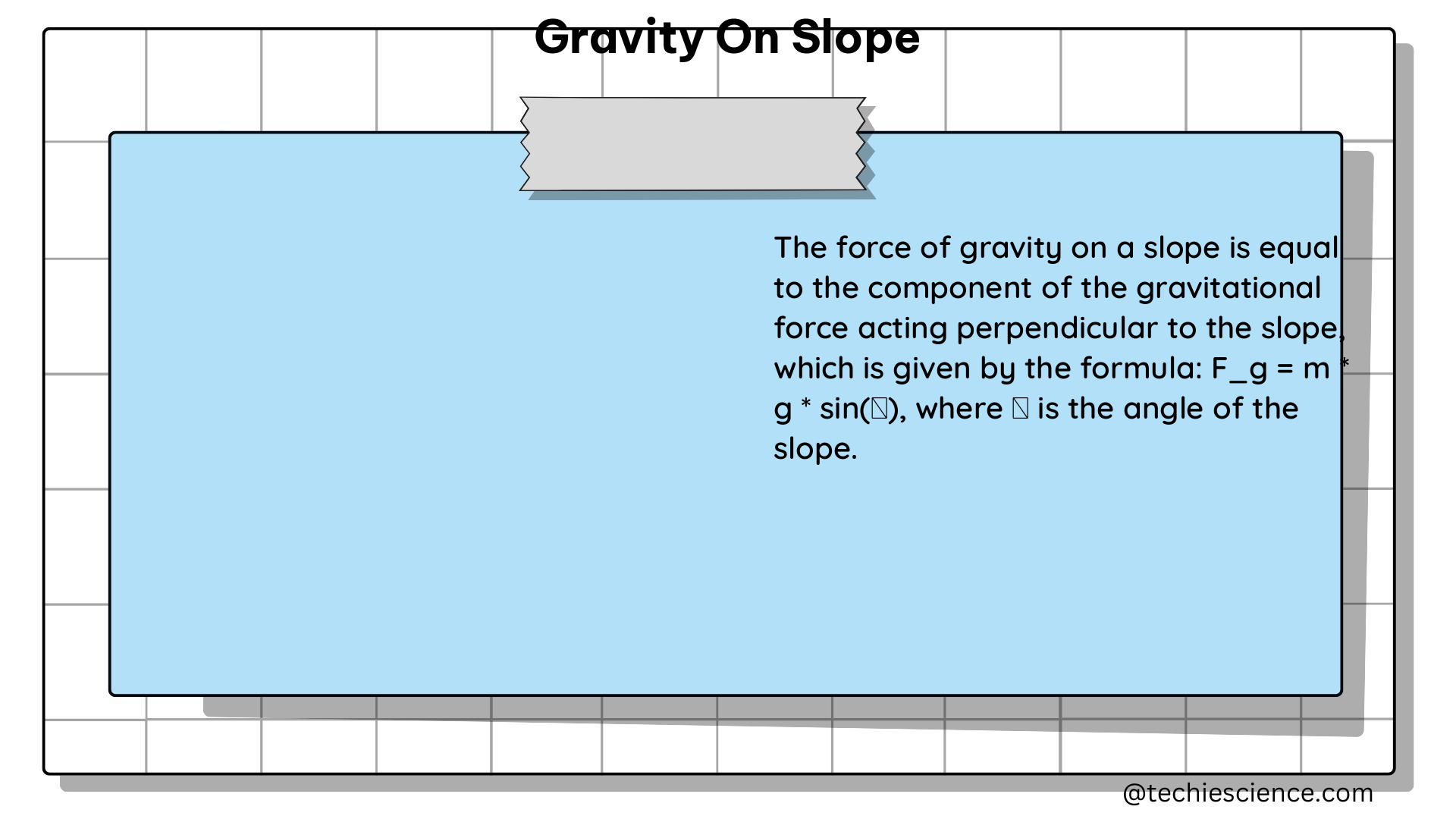
When considering the effect of gravity on a slope, we need to take into account the angle of the slope. The formula for calculating the acceleration due to gravity on a slope (g’) is:
g' = g * cos(θ)
where:
– g' is the acceleration due to gravity on a slope
– g is the acceleration due to gravity on a level surface
– θ is the angle of the slope
This formula demonstrates that the acceleration due to gravity on a slope is less than the acceleration due to gravity on a level surface, and the angle of the slope directly affects the value of g'.
Example Calculation
Let’s consider an example where the acceleration due to gravity on a level surface (g) is 9.8 m/s² and the angle of the slope (θ) is 30 degrees.
Using the formula:
g' = g * cos(θ)
g' = 9.8 * cos(30°)
g' = 8.5 m/s²
This means that the acceleration due to gravity on the 30-degree slope is 8.5 m/s².
Force of Gravity on a Slope (F)
In the case of Frank, who is trying to calculate the force of gravity from his lab data, he can use the following formula:
F = m * g'
where:
– F is the force of gravity
– m is the mass of the ball
– g' is the acceleration due to gravity on the slope
To calculate g' from his data, Frank can use the following formula:
g' = (4 * a * d) / (l * sin(2θ))
where:
– a is the acceleration of the ball
– d is the distance traveled by the ball
– l is the length of the inclined plane
– θ is the angle of the inclined plane
By using these formulas, Frank can determine the acceleration due to gravity on the slope and then calculate the force of gravity acting on the ball.
Additional Data Points and Facts
Here are some additional data points and facts related to gravity on a slope:
-
Angle of the Slope: The angle of the slope has a significant impact on the acceleration due to gravity on the slope. As the angle of the slope increases, the value of
g'decreases. -
Friction: In real-world scenarios, friction between the object and the inclined plane can affect the acceleration and the force of gravity. This factor should be considered when analyzing the system.
-
Potential Energy: As an object moves down an inclined plane, its potential energy decreases, and this energy is converted into kinetic energy. The rate of change in potential energy is directly related to the force of gravity on the slope.
-
Numerical Examples: Providing specific numerical examples with step-by-step calculations can help students better understand the application of the formulas and the impact of different parameters on the final results.
-
Experimental Data: Presenting experimental data, such as measurements of distance, time, and acceleration, can further reinforce the concepts and allow students to practice applying the formulas to real-world scenarios.
-
Graphical Representations: Incorporating graphs or diagrams that illustrate the relationship between the angle of the slope, the acceleration due to gravity, and the force of gravity can enhance the visual understanding of the topic.
-
Practical Applications: Discussing practical applications of gravity on a slope, such as in the design of roller coasters, ski slopes, or transportation systems, can help students appreciate the relevance of this concept in the real world.
Conclusion
Gravity on a slope is a fundamental concept in physics that has far-reaching applications. By understanding the underlying principles, formulas, and practical considerations, physics students can develop a comprehensive understanding of this topic and apply it to various real-world scenarios. This guide has provided a detailed exploration of the subject, including Galileo’s Inclined Plane Experiment, the calculation of acceleration due to gravity on a slope, and the determination of the force of gravity. With the additional data points and facts presented, students can deepen their knowledge and become proficient in this essential area of physics.
References
- Galileo’s Inclined Plane Experiment – Maple Help – Maplesoft
- Gravity with Galileo’s inclined plane? – Physics Forums
- Physics 1 Lab: Determining ‘g’ on an Incline – YouTube
Hi, I’m Akshita Mapari. I have done M.Sc. in Physics. I have worked on projects like Numerical modeling of winds and waves during cyclone, Physics of toys and mechanized thrill machines in amusement park based on Classical Mechanics. I have pursued a course on Arduino and have accomplished some mini projects on Arduino UNO. I always like to explore new zones in the field of science. I personally believe that learning is more enthusiastic when learnt with creativity. Apart from this, I like to read, travel, strumming on guitar, identifying rocks and strata, photography and playing chess.