An octahedron is a three-dimensional geometric shape that consists of eight equilateral triangles. It is one of the five Platonic solids, which are regular, convex polyhedra. The octahedron has a total of six vertices and twelve edges. Each vertex is connected to four other vertices, forming a symmetrical structure. This shape is commonly found in nature, such as in the structure of certain crystals. It is also used in various fields, including architecture, engineering, and mathematics. The octahedron’s symmetrical properties make it an interesting and versatile shape to study and work with.
Key Takeaways
| Property | Value |
|---|---|
| Number of Faces | 8 |
| Number of Edges | 12 |
| Number of Vertices | 6 |
| Symmetry | Symmetrical |
| Shape Type | Platonic Solid |
Understanding Octahedron: Definition and Basics
An octahedron is a geometric shape that falls under the category of polyhedra. It is a three-dimensional figure with eight faces, twelve edges, and six vertices. The term “octahedron” is derived from the Greek words “octa” meaning eight and “hedra” meaning face.
Meaning of Octahedron
In mathematics and geometry, an octahedron is classified as a Platonic solid. This means that it is a regular polyhedron with identical faces, edges, and vertices. The octahedron is unique among the five Platonic solids as it has the fewest number of faces. It can be visualized as two pyramids placed base to base, creating a symmetrical shape.
The octahedron is closely related to other polyhedra, such as the cube, tetrahedron, icosahedron, and dodecahedron. It shares certain characteristics with these shapes, but its distinct feature is the presence of eight triangular faces. Each vertex of the octahedron connects to four edges, and each edge is shared by two faces. This arrangement gives the octahedron its characteristic symmetrical structure.
Octahedron in Mathematics and Geometry
In the realm of mathematics and geometry, the octahedron holds significance as a mathematical model and a fundamental shape in spatial geometry. It is a convex polyhedron, meaning that all its faces are flat and its internal angles are less than 180 degrees. The regular octahedron, with equilateral triangles as its faces, is particularly studied for its symmetrical properties.
The octahedron also has a dual polyhedron, known as the cube. The vertices of the octahedron correspond to the faces of the cube, and vice versa. This duality highlights the relationship between these two shapes and their shared characteristics.
Octahedron in Chemistry
In the field of chemistry, the octahedron plays a significant role in crystal structures and molecular geometry. It is commonly observed in compounds with an octahedral coordination geometry, where six ligands surround a central atom. This arrangement creates an octahedral symmetry, with the ligands positioned at the vertices of an octahedron.
The octahedron’s symmetrical nature and its ability to pack efficiently make it a key component in various crystal lattices and molecular structures. It is also utilized in the study of tiling and mirror symmetry, further highlighting its importance in the field of chemistry.
Characteristics of Octahedron
An octahedron is a geometric shape and a type of polyhedron. It is a three-dimensional figure with eight faces, twelve edges, and six vertices. The word “octahedron” is derived from the Greek words “octa” meaning eight and “hedra” meaning face.
Is Octahedron a Solid?
Yes, an octahedron is a solid. It is a regular polyhedron, which means all of its faces are congruent regular polygons. In the case of an octahedron, each face is an equilateral triangle. The regular octahedron is one of the five Platonic solids, which are the only five regular polyhedra in geometry.
Octahedron as a Platonic Solid
As mentioned earlier, the octahedron is one of the five Platonic solids. The Platonic solids are highly symmetrical three-dimensional shapes. Along with the octahedron, the other Platonic solids are the cube, tetrahedron, icosahedron, and dodecahedron. Each Platonic solid has its own unique characteristics and properties.
Is Octahedron Convex?
Yes, an octahedron is a convex polyhedron. A convex polyhedron is a solid where any line segment connecting two points within the shape lies entirely inside the shape. In the case of an octahedron, all of its faces are triangles, and any line segment connecting two points within the octahedron will remain within its boundaries.
Structure of Octahedron

Faces, Edges, and Vertices of Octahedron
The octahedron is a geometric shape and a polyhedron. It is one of the five Platonic solids, which are regular polyhedra with identical faces, edges, and vertices. The octahedron has eight faces, twelve edges, and six vertices. Each face of the octahedron is an equilateral triangle, and all the faces are congruent to each other. The edges of the octahedron are the line segments where the faces meet, and the vertices are the points where three edges intersect.
To better understand the structure of an octahedron, let’s take a closer look at its shape and appearance.
Octahedron Shape and Appearance
The octahedron has a unique shape that is visually captivating. It resembles two pyramids placed base to base, creating a symmetrical and balanced structure. The octahedron is often described as a three-dimensional shape that resembles a cube with its corners cut off. It can also be seen as a dual polyhedron to the cube, as each vertex of the octahedron corresponds to the center of a face of the cube, and vice versa.
In terms of spatial geometry, the octahedron belongs to the trigonal system, which is characterized by threefold symmetry. Its crystal structure is often compared to the diamond structure, as both exhibit octahedral symmetry. The octahedron is a convex polyhedron, meaning that all its internal angles are less than 180 degrees.
Does an Octahedron have Parallel Lines?
No, an octahedron does not have parallel lines. In an octahedron, each edge connects two vertices, and no two edges are parallel to each other. The octahedron’s faces are composed of triangles, and each triangle is a plane figure. However, the planes of the triangles are not parallel to each other. Therefore, an octahedron does not exhibit parallel lines within its structure.
Types of Octahedron
An octahedron is a geometric shape and a polyhedron with eight faces. It is one of the five Platonic solids, which are regular polyhedra with identical faces, edges, and vertices. The octahedron is a fascinating three-dimensional shape that exhibits symmetry and is closely related to other polyhedra such as the cube, tetrahedron, icosahedron, and dodecahedron.
Regular Octahedron
The regular octahedron is a specific type of octahedron that has several unique characteristics. It is a convex polyhedron with six vertices and twelve edges. Each face of a regular octahedron is an equilateral triangle, and all the faces are congruent. The regular octahedron is a symmetrical figure that possesses octahedral symmetry, meaning it has rotational and reflectional symmetry along various planes.
Irregular Octahedron
Unlike the regular octahedron, an irregular octahedron does not have congruent faces or equal edge lengths. It is a more general term used to describe any octahedron that does not meet the criteria of a regular octahedron. Irregular octahedra can have faces that are different shapes and sizes, resulting in a more varied and asymmetrical appearance.
Truncated Octahedron
The truncated octahedron is a fascinating variation of the octahedron that is obtained by truncating the vertices of a regular octahedron. This process involves cutting off the corners of the regular octahedron, resulting in a polyhedron with both triangular and hexagonal faces. The truncated octahedron has a total of 14 faces, 36 edges, and 24 vertices.
Octahedron in Real Life
The octahedron is a fascinating geometric shape that can be found in various aspects of our everyday lives. With its eight faces and symmetrical structure, the octahedron is classified as a polyhedron and is one of the five Platonic solids. Its unique geometry and symmetry make it a captivating subject in the field of mathematics and spatial geometry.
Octahedron Minerals and Crystals
In the world of minerals and crystals, the octahedron is a common and visually striking form. Many minerals naturally crystallize into octahedral shapes due to their crystal structure and the arrangement of atoms within them. Some examples of minerals that commonly exhibit octahedral crystals include diamond, fluorite, magnetite, and spinel.
The octahedral shape of these minerals is characterized by six vertices, twelve edges, and eight equilateral triangular faces. The regular octahedron is a specific type of octahedron where all the faces are congruent and the angles between the faces are equal. This regularity adds to the aesthetic appeal of octahedral crystals.
Octahedron Examples in Real Life
Apart from minerals and crystals, the octahedron can also be observed in various real-life objects and structures. Let’s explore some examples:
Diamonds: Diamonds, known for their brilliance and beauty, have a crystal structure that is based on an octahedral arrangement. The carbon atoms in a diamond are arranged in a three-dimensional lattice, forming an octahedral shape.
Traffic Cones: Have you ever noticed the shape of a traffic cone? It is essentially an octahedron with the top cut off. The octahedral shape provides stability and visibility, making it an ideal design for directing traffic.
Snowflakes: While snowflakes come in a variety of intricate patterns, some snowflakes exhibit an octahedral symmetry. The six arms of the snowflake form an octahedral shape, showcasing the beauty of symmetry in nature.
Molecular Models: In the field of chemistry, molecular models are often used to represent the three-dimensional structure of molecules. Octahedral compounds, such as some transition metal complexes, have a central atom surrounded by six ligands arranged in an octahedral shape.
Architecture: The octahedron has also found its way into architectural designs. From modern sculptures to futuristic buildings, architects have incorporated the octahedral form to create visually striking structures that play with light and shadow.
By exploring these examples, we can see how the octahedron is not just a mathematical model but also a shape that has practical applications in various fields. Its symmetrical and geometric properties make it an intriguing figure that continues to inspire creativity and innovation.
Remember, the octahedron is just one of the many fascinating polyhedra in the world of geometry. Its relationship with other polyhedra like the cube, tetrahedron, icosahedron, and dodecahedron adds to the richness of spatial geometry and the study of three-dimensional shapes.
Making an Octahedron
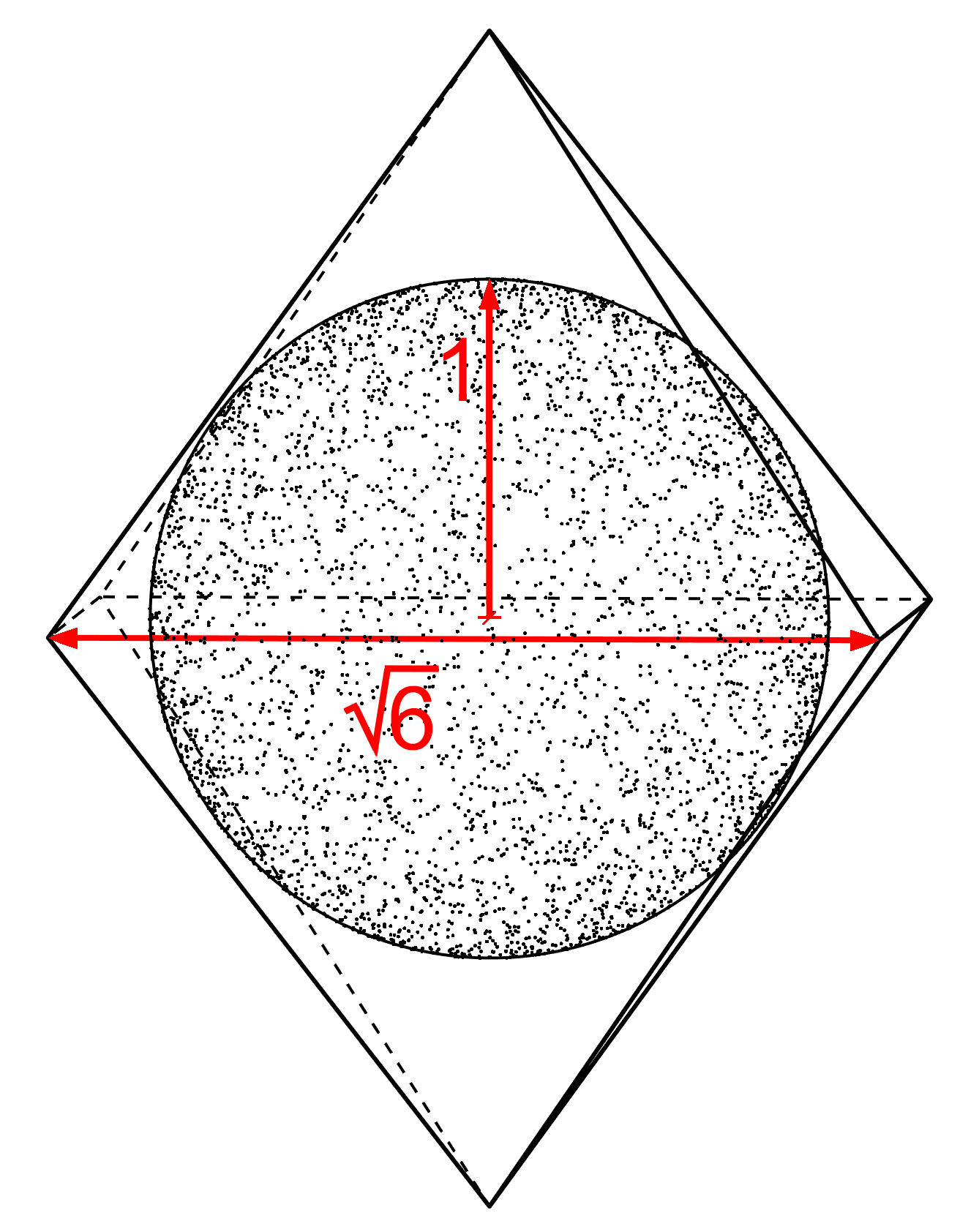
An octahedron is a geometric shape and a polyhedron with eight faces. It is one of the five Platonic solids, which are regular polyhedra with equal faces, edges, and vertices. The octahedron is a fascinating three-dimensional shape that exhibits symmetry and can be found in various fields of study, including geometry, crystal structures, and spatial geometry.
Octahedron Template and Net
To create an octahedron, you can start with a template or net. A net is a two-dimensional representation of a three-dimensional shape that can be folded to form the desired polyhedron. In the case of an octahedron, the net consists of eight equilateral triangles.
Here is an example of an octahedron net:
/
/__
/ /
/__/__
You can print out this net and follow the folding instructions to construct your octahedron. Make sure to fold along the lines and secure the edges to create a sturdy structure.
Making Octahedron with Paper and Cardboard
If you prefer a hands-on approach, you can make an octahedron using paper or cardboard. Start by cutting out eight identical equilateral triangles. You can use a ruler and a protractor to ensure accurate measurements.
Once you have the triangles, fold along the edges to create creases. Then, carefully assemble the triangles by attaching the edges together. You can use glue or tape to secure the connections. Make sure all the triangles are aligned properly to form a regular octahedron.
Octahedron Origami
Origami, the art of paper folding, offers another creative way to make an octahedron. By following specific folding techniques, you can transform a single sheet of paper into a beautiful octahedral structure.
Origami octahedrons can be made using various folding patterns, such as the waterbomb base or the blintz fold. These techniques involve precise folds and manipulations to achieve the desired shape. With practice and patience, you can create stunning origami octahedrons to display or use as decorative pieces.
Mathematical Properties of Octahedron
An octahedron is a geometric shape that falls under the category of polyhedra. It is a three-dimensional figure with eight faces, making it one of the five Platonic solids. The octahedron has a unique symmetry and is closely related to other polyhedra such as the cube, tetrahedron, icosahedron, and dodecahedron.
Octahedron Volume and Formula
To calculate the volume of an octahedron, we can use the following formula:
Volume = (2 * sqrt(2) * a^3) / 3
Where ‘a’ represents the length of the edge of the octahedron. The volume of an octahedron can be thought of as two tetrahedra joined together at their bases.
Octahedron Surface Area
The surface area of an octahedron can be determined by summing the areas of its individual faces. Each face of an octahedron is an equilateral triangle, so we can calculate the surface area using the following formula:
Surface Area = 2 * sqrt(3) * a^2
Where ‘a’ represents the length of the edge of the octahedron. The surface area of an octahedron is twice the area of one of its faces.
Octahedron in Culture and Spirituality
The octahedron is a fascinating geometric shape that holds significant cultural and spiritual meaning. As a polyhedron with eight faces, it is classified as a Platonic solid, a group of five regular polyhedra that have equal faces, edges, and vertices. Its symmetrical structure and unique properties have made it a subject of interest in various fields, including art, design, and spirituality.
Octahedron Spiritual Meaning
In many spiritual traditions, the octahedron is associated with balance, harmony, and transformation. Its geometry represents the interconnectedness of all things and the equilibrium between opposing forces. The octahedron’s shape resembles two pyramids, with their bases joined together, forming a three-dimensional figure with six vertices and twelve edges. This characteristic makes it a symbol of unity and integration.
The octahedron is often linked to the element of air and is believed to enhance mental clarity, intuition, and spiritual growth. Its geometric structure is said to facilitate the flow of energy and promote a sense of equilibrium within oneself and the surrounding environment. Some practitioners use octahedron-shaped crystals or meditate with octahedron imagery to connect with these spiritual qualities.
Octahedron in Art and Design
The octahedron’s aesthetic appeal and mathematical elegance have made it a popular motif in art and design. Its symmetrical form and clean lines make it visually pleasing and versatile for various creative applications. Artists and designers often incorporate octahedron-inspired patterns, sculptures, and jewelry into their work to add a touch of geometric beauty.
In architecture, the octahedron can be seen in the design of buildings and structures. Its regular shape and balanced proportions create a sense of stability and harmony. The octahedron’s spatial geometry and Euclidean properties make it an intriguing element to explore in architectural design, both in its pure form and as part of more complex compositions.
The octahedron also has a unique relationship with other geometric shapes. It is the dual polyhedron of the cube, meaning that the vertices of one shape correspond to the faces of the other. This duality creates a fascinating interplay between the octahedron and the cube, highlighting the interconnectedness of different mathematical models and spatial figures.
What is the relationship between octahedron and nonagon? How are the secrets of nonagons discovered?
The octahedron and nonagon are both geometric shapes with unique properties. While the octahedron is a polyhedron with eight faces, the nonagon is a polygon with nine sides. Despite their different structures, these two shapes can intersect in intriguing ways. By exploring the secrets of nonagons, such as their symmetry and angles, we can uncover a deeper understanding of their relationship to the octahedron. To delve into the mysteries of nonagons, “Discover the secrets of nonagons” provides valuable insights and knowledge on their properties, construction methods, and mathematical significance.
Frequently Asked Questions
1. What is an octahedron?
An octahedron is a geometric shape and a type of polyhedron that has eight faces, six vertices, and twelve edges. It is one of the five Platonic solids and exhibits perfect symmetry, making it a regular polyhedron.
2. How does an octahedron look like?
An octahedron appears as a three-dimensional shape with eight equilateral triangle faces. It has six vertices where the faces meet and twelve edges. Its appearance can be thought of as two square pyramids with their bases glued together.
3. What is a regular octahedron and how is it different from an irregular octahedron?
A regular octahedron is a symmetrical geometric figure with all its faces being equilateral triangles. It has six vertices and twelve edges. An irregular octahedron, on the other hand, does not have all faces as equilateral triangles and lacks the perfect symmetry of a regular octahedron.
4. What are some examples of an octahedron in real life?
Octahedrons can be found in nature and in man-made structures. A common example is the crystal structure of a diamond, which is based on repeating octahedrons. Additionally, some dice used in board games are shaped as octahedrons.
5. Is an octahedron a solid?
Yes, an octahedron is a solid figure in three-dimensional Euclidean space. It is a type of polyhedron, which means it is a three-dimensional shape with flat faces and straight edges.
6. How many faces, edges, and vertices does an octahedron have?
An octahedron has eight faces, twelve edges, and six vertices. Each vertex is the point where three edges meet, and each face is an equilateral triangle in a regular octahedron.
7. What is the volume of an octahedron?
The volume of a regular octahedron can be calculated using the formula V = (sqrt(2) / 3) * a³ where ‘a’ is the length of an edge.
8. Is an octahedron a prism or a pyramid?
An octahedron is neither a prism nor a pyramid. It is a type of Platonic solid, a category of geometric shapes distinct from prisms and pyramids. While it might resemble two pyramids stuck together at their bases, it forms its own unique category.
9. Does an octahedron have parallel faces?
Yes, an octahedron does have parallel faces. Each face is parallel to the one directly opposite to it.
10. How to make an octahedron with paper or cardboard?
To make an octahedron, you would need to cut out eight equilateral triangles from the paper or cardboard. Then, arrange and stick four of them edge to edge to form the base. Attach the remaining four triangles to each edge of a base triangle, and then fold them up and stick their edges together. You should end up with a three-dimensional shape with eight triangular faces – an octahedron.
Also Read:
- Stratosphere 2
- Is a carbohydrate a monomer or polymer
- Ultraviolet catastrophe
- Quotient rule
- Trebuchet vs catapult vs ballista
- Dioptric power
- Tsunami the most devastating calamity
- Homogeneous mixture
- How are nucleotides produced
- How much does a gallon of milk weigh

The TechieScience Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the TechieScience.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.
