In electromagnetism, the terms magnetic flux and magnetic flux density are constantly used. Here, a detailed analysis on both these terms is given.
Magnetic field behaviors, in any context, are well explained by magnetic flux, a scalar and magnetic flux density, a vector. Magnetic flux density gives an estimate of the magnetic flux per unit area or rather; magnetic flux is the scalar product of magnetic flux density and the area vector.
Some important facts on magnetic flux and magnetic flux density can be found below.
What is magnetic flux density?
Magnetic flux is a term that occurs more often in magnetism. Most of us are unaware of magnetic flux density which is quite different from magnetic flux.
Consider an area element placed perpendicular to a magnetic field. Then the amount of magnetic flux that passes through the given unit area is referred to as magnetic flux density. Magnetic flux density is quantity that has both magnitude and direction, and is expressed in units of Tesla(T) in SI system.
Magnetic induction is often another term used to refer to magnetic flux density. Biot-Savart law is often used to determine the magnetic flux density at any given point due to a current-carrying wire.
How to calculate magnetic flux density?
In a constant magnetic field, magnetic flux is mathematically expressed as follows:
ɸ=B.S
or.
ɸ=BScosθ
where,
ɸ is the magnetic flux in webers
B denotes the magnetic flux density in units of tesla
S is the area in square meters
θ is the angle made by the magnetic field with the area vector (normal to the surface)
Rearranging the terms in the above expression, we get the magnetic flux density,
B=ɸ/Scosθ
When the magnetic field lines are perpendicular to the area under consideration, the expression becomes
B=ɸ/S
Another way to calculate magnetic flux density around a current carrying wire is using Biot-Savart’s law.
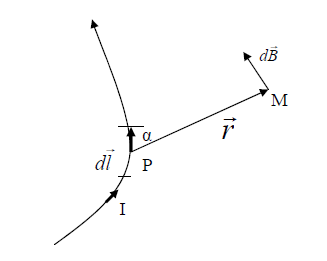
Image Credits: Wikimedia Commons
The statement of Biot-Savart’s law is mathematically represented as

where,
dB is the magnetic flux density
μ0 is the magnetic permeability in air
I is the current flowing through the wire
dl is the length element
r is the perpendicular distance from the current element to the point where magnetic flus density is to be found.
Yet another way to determine magnetic flux density is from magnetic field strength in a medium. Magnetic flux density of any material medium can be equivalently represented by the product of the magnetic permeability of the medium μ and magnetic field strength (H).
B=μH
Are magnetic flux and magnetic flux density same?
No, magnetic flux and magnetic flux density are two different quantities, one a scalar and another a vector and this is clearly evident from the discussions made till now.
How are magnetic flux and magnetic flux density related?
Magnetic flux is represented as the scalar product or dot product of magnetic flux density and the area perpendicular to the magnetic field direction.
ɸ=B.S
More general representation goes this way, where magnetic flux is the integral of the dot product of magnetic flux density and the infinitesimal area to which magnetic field lines are perpendicular.

The mathematical expressions gives an insight on how magnetic flux turns out to be a scalar. It is a mathematical law that dot product of two vectors yield a scalar. Hence, here magnetic flux density B and area S being vector quantities, their dot product yields a scalar, magnetic flux ɸ.
Difference between magnetic flux and magnetic flux density.
From the discussions made till now, we can easily point out few general differences between magnetic flux and magnetic flux density.
- Magnetic flux is a physical quantity that gives an estimate of the number of magnetic field lines that passes perpendicular to a given surface, while magnetic flux density is equivalently the amount of magnetic flux per unit area.
- Magnetic flux has only magnitude but no direction, that is, it is a scalar quantity. Whereas magnetic flux density or magnetic induction can be represented with both magnitude and direction, hence a vector quantity.
- Over a closed surface, magnetic flux is always zero. For each point on the closed surface, there is a definite value of magnetic flux density and it varies for different points.
On the other hand, the number of magnetic field lines entering and leaving the closed surface as a whole, is the same and hence, the net magnetic flux is equal to zero over the closed surface.
Numericals Based On Magnetic Flux And Magnetic Flux Density
Numerical 1: Consider a square loop whose side is 4 cm long and is positioned in a uniform magnetic field B of 1.0 T such that the plane of the loop makes an angle of 30 degrees with the magnetic field. Determine the magnetic flux passing through the square loop.
Solution: The diagrammatic representation of the given problem is shown aside.

Given, length of the square loop = 4 cm =0.04 m
The magnitude of magnetic field B = 1.0 T
The angle made by the plane of loop with magnetic field lines = 30 degrees
Hence the angle made by the magnetic field and normal to the loop θ= 90 – 30 = 60 degrees
We know that flux through any surface is given by
ɸ=B.S=BScosθ
Here S = area of the square loop = 0.04*0.04 = 0.0016 m2
Therefore,ɸ=1.0*0.0016*Cos 60=0.008W
Hence the required value of magnetic flux through the loop is 0.0008 W or 0.8 mW.
Note: To avoid mistakes, care has to be taken while using the value of theta. Theta must always be taken with reference to the perpendicular to the area under consideration.
In this example, the given 30 degrees is angle made by magnetic field with the plane or surface of loop and not its perpendicular. Hence the value of theta is 60 degrees.
Numerical 2: In a uniform magnetic field whose strength is unknown, a circular loop of a radius of 5 cm is placed perpendicularly. The magnetic flux through the loop is found to be 10 mW.
- Determine the magnetic flux density.
- Now if the magnetic field is rotated by 90 degrees such that the field lines are parallel to the surface of the loop, estimate the value of magnetic flux through the loop.
Solution:
Given,
The radius of the circular loop r = 5 cm = 0.05 m
Also, the magnetic flux through the loop = phi = 10 mW = 0.01 W
Since radius is given, we have area of the loop as S=πr2
Therefore, S = π*(0.05)2
It is mentioned that the loop is placed perpendicular to the magnetic field. Hence θ = 0 degrees
Since we know the relation

Hence the magnetic flux density is 1.273 T.
Now, for the part(b) of the question, the angle becomes 90 degree and hence using the obtained value of magnetic flux,
ɸ=B.S=BScosθ
ɸ=1.273*π*(0.05)2 cos 90
ɸ= 0 W
The result suggests that the magnetic flux is zero when the magnetic field lines are parallel to the surface.
Summary
To wind up, we have dealt with magnetic flux and magnetic flux density in this post. A more comprehensive description is provided detailing several facts like the difference between magnetic flux and magnetic flux density as well as including numericals that helps to analyze the concept more practically.
Read more about
Also Read:
- How is magnetic field produced
- Magnetic field lines of earth
- Is static electricity magnetic
- Is gravity electromagnetic
- Is titanium magnetic
- Magnetic field between two parallel wires
- Is brass magnetic
- Is mirror magnetic
- Is gallium magnetic
- Magnetic field and time
Hello, I am Deeksha Dinesh, currently pursuing post-graduation in Physics with a specialization in the field of Astrophysics. I like to deliver concepts in a simpler way for the readers.
