Magnetic Field Between Two Parallel Wires (9 Facts )

The magnetic field between two parallel wires is a fascinating phenomenon that occurs when electric currents flow through the wires. When two wires are placed parallel to each other and carry electric currents in the same direction, they create a magnetic field that interacts with each other. This interaction results in a magnetic force between the wires, causing them to either attract or repel each other, depending on the direction of the current. The strength of the magnetic field is determined by factors such as the distance between the wires, the magnitude of the current, and the permeability of the medium.

Key Takeaways

Distance between wires	Magnetic field strength
Closer	Stronger
Farther	Weaker
Same direction	Attraction
Opposite direction	Repulsion

Understanding Magnetic Fields

Definition and Explanation of Magnetic Fields

Magnetic fields are an integral part of our everyday lives, even though we may not always be aware of their presence. They play a crucial role in various natural phenomena and technological applications. In simple terms, a magnetic field is a region in space where magnetic forces can be detected. These forces are exerted on magnetic objects, such as iron or steel, and can cause them to move or align in a particular direction.

To understand magnetic fields better, let’s consider the example of a bar magnet. A bar magnet has two poles – a north pole and a south pole. When we bring two bar magnets close to each other, we observe that opposite poles attract each other, while like poles repel each other. This phenomenon is due to the presence of magnetic fields around the magnets.

The strength and direction of a magnetic field can be influenced by several factors. Let’s explore some of these factors:

Current-Carrying Wires: When an electric current flows through a wire, it generates a magnetic field around it. The magnetic field produced by a current-carrying wire can be determined using the Biot-Savart law. This law states that the magnetic field at a point is directly proportional to the current flowing through the wire and inversely proportional to the distance from the wire.

For example, consider two parallel wires carrying currents in the same direction. The magnetic field between these wires will be stronger compared to the magnetic field outside the wires. The magnetic field lines will be concentric circles around each wire, with the direction of the magnetic field determined by the right-hand rule.

Ampere’s Law: Ampere’s law relates the magnetic field around a closed loop to the electric current passing through the loop. It states that the line integral of the magnetic field around a closed loop is equal to the product of the current enclosed by the loop and a constant called the permeability of free space.

For instance, if we have a loop of wire carrying a current, the magnetic field inside the loop can be calculated using Ampere’s law. This law helps us understand the relationship between the current-carrying wire and the magnetic field it produces.

magnetic field between two parallel wire

Distance between Current-Carrying Wires: The distance between two parallel current-carrying wires also affects the magnetic field between them. As the distance between the wires decreases, the magnetic field strength increases. This relationship can be explained by the inverse square law, which states that the magnetic field strength is inversely proportional to the square of the distance between the wires.

For example, if we have two parallel wires carrying currents in the same direction and we decrease the distance between them, the magnetic field between the wires will become stronger. This phenomenon is important to consider in applications such as transformers and electrical circuits.

Orientation and Angle of Current-Carrying Wires: The orientation and angle between two current-carrying wires can also influence the magnetic field between them. When the wires are parallel and the currents flow in the same direction, the magnetic fields add up, resulting in a stronger combined magnetic field. On the other hand, if the currents flow in opposite directions, the magnetic fields cancel each other out, resulting in a weaker combined magnetic field.

For instance, if we have two wires carrying currents in opposite directions, the magnetic fields they produce will be in opposite directions. This can lead to attractive or repulsive forces between the wires, depending on the distance and current strength.

Understanding the factors that influence magnetic fields is essential in various fields, including electrical engineering, physics, and magnetism. By studying these factors and their effects, scientists and engineers can design and optimize devices such as motors, generators, and magnetic resonance imaging (MRI) machines.

Remember, magnetic fields are all around us, shaping our world and enabling countless technological advancements. So the next time you encounter a magnet or a current-carrying wire, take a moment to appreciate the invisible forces at play and the fascinating world of magnetic fields.

Magnetic Field Between Two Parallel Wires

Explanation of the magnetic field between two parallel wires

The magnetic field between two parallel wires is a fascinating phenomenon that occurs when electric currents flow through the wires. When current flows through a wire, it creates a magnetic field around it. In the case of two parallel wires, the magnetic fields interact with each other, resulting in a magnetic force between the wires.

To understand this concept better, let’s consider two parallel wires carrying electric currents in the same direction. According to Ampere’s law and the Biot-Savart law, the magnetic field produced by each wire can be calculated using the following equation:

$B = frac{{mu_0 cdot I}}{{2 cdot pi cdot r}}$

Where: – B is the magnetic field strength – (mu_0) is the permeability of free space (a constant value) – I is the current flowing through the wire – r is the distance from the wire

The magnetic field lines around each wire form concentric circles, with the direction of the magnetic field determined by the right-hand rule. The magnetic field lines are closer together near the wires and spread out as they move away.

When two parallel wires carry currents in the same direction, the magnetic field lines around each wire interact with each other. The magnetic field lines due to one wire exert a force on the other wire, causing them to attract each other. This force is strongest when the wires are close together and decreases as the distance between them increases.

On the other hand, if the currents in the two wires are flowing in opposite directions, the magnetic field lines around each wire will be in opposite directions as well. In this case, the magnetic fields repel each other, resulting in a repulsive force between the wires.

It’s important to note that the magnetic field between two parallel wires is dependent on various factors, including the current flowing through the wires, the distance between the wires, and the direction of the currents. Let’s explore these factors further.

Factors affecting the magnetic field between two parallel wires

Current: The strength of the magnetic field between two parallel wires is directly proportional to the current flowing through the wires. A higher current will result in a stronger magnetic field and a greater magnetic force between the wires.
Distance: The distance between the two parallel wires also affects the magnetic field strength. As the distance increases, the magnetic field between the wires weakens. This is because the magnetic field lines spread out and become less concentrated as they move away from the wires.
Direction of Currents: The direction of the currents flowing through the wires plays a crucial role in determining the magnetic field interaction. When the currents flow in the same direction, the magnetic fields attract each other. Conversely, when the currents flow in opposite directions, the magnetic fields repel each other.

To illustrate the effect of these factors, let’s consider an example. Suppose we have two parallel wires, each carrying a current of 2 Amperes. The distance between the wires is 0.5 meters. Using the magnetic field equation mentioned earlier, we can calculate the magnetic field strength at a point between the wires.

$B = frac{{mu_0 cdot I}}{{2 cdot pi cdot r}}$

Let’s assume we want to find the magnetic field strength at a point located 0.2 meters away from one of the wires. Plugging in the values into the equation, we get:

$B = frac{{4pi times 10^{-7} cdot 2}}{{2 cdot pi cdot 0.2}}$

Simplifying the equation, we find that the magnetic field strength at that point is 0.02 Tesla.

By understanding the magnetic field between two parallel wires and the factors that affect it, we can gain insights into the behavior of current-carrying wires and the forces they exert on each other. This knowledge is essential in various fields, including electrical engineering and physics.

Magnetic Field Direction and Strength

Understanding the direction of the magnetic field between two parallel wires

When two parallel wires carry electric currents, they create magnetic fields around them. Understanding the direction of the magnetic field between these wires is crucial in various applications, such as designing electrical circuits and electromagnets. The direction of the magnetic field can be determined using the right-hand rule.

To apply the right-hand rule, follow these steps:

Extend your right hand and point your thumb in the direction of the current in the first wire.
Curl your fingers towards the second wire.
The direction in which your fingers curl represents the direction of the magnetic field between the two wires.

Let’s consider an example to illustrate this concept. Suppose we have two parallel wires, Wire A and Wire B, with currents flowing in opposite directions. If the current in Wire A is flowing upwards and the current in Wire B is flowing downwards, we can use the right-hand rule to determine the direction of the magnetic field between them. By pointing our thumb upwards for the current in Wire A and curling our fingers towards Wire B, we find that the magnetic field is directed towards us.

Determining the strength of the magnetic field between two parallel wires

The strength of the magnetic field between two parallel wires can be calculated using Ampere’s law or the Biot-Savart law. Ampere’s law relates the magnetic field to the current enclosed by a closed loop, while the Biot-Savart law calculates the magnetic field at a specific point due to a current-carrying wire.

To calculate the magnetic field strength between two parallel wires, we can use the Biot-Savart law. The formula for the magnetic field at a point P, located at a distance ‘r’ from a current-carrying wire, is given by:

$B = frac{{mu_0 cdot I}}{{2pi cdot r}}$

Where: – B is the magnetic field strength – (mu_0) is the permeability of free space (a constant value) – I is the current flowing through the wire – r is the distance from the wire to the point P

Let’s work through an example to understand how to calculate the magnetic field strength between two parallel wires. Suppose we have two parallel wires, Wire A and Wire B, separated by a distance of 0.1 meters. Wire A carries a current of 2 Amperes, while Wire B carries a current of 3 Amperes. We want to determine the magnetic field strength at a point located 0.05 meters away from Wire A.

Using the formula, we can substitute the given values into the equation:

$B = frac{{4pi times 10^{-7} cdot 2}}{{2pi cdot 0.05}}$

Simplifying the equation, we find:

$B = 8 times 10^{-6} , text{T}$

Therefore, the magnetic field strength between the two parallel wires at the given point is 8 microteslas.

By understanding the direction and calculating the strength of the magnetic field between two parallel wires, we can gain insights into the behavior of current-carrying wires and their magnetic interactions. This knowledge is essential in various fields, including electrical engineering, physics, and magnetism.

Magnetic Field Lines of Two Parallel Wires

Explanation of Magnetic Field Lines

Magnetic field lines are a visual representation of the magnetic field surrounding a current-carrying wire. They provide a way to understand the direction and strength of the magnetic field at different points in space. When two parallel wires carry electric currents, they create magnetic fields that interact with each other.

To understand the concept of magnetic field lines, let’s consider two parallel wires, Wire A and Wire B, carrying currents in the same direction. According to Ampere’s law and the Biot-Savart law, the magnetic field produced by Wire A at a point P is directly proportional to the current flowing through Wire A and inversely proportional to the distance between Wire A and point P. Similarly, the magnetic field produced by Wire B at point P is determined by the current flowing through Wire B and the distance between Wire B and point P.

The magnetic field lines around Wire A and Wire B are circular and concentric. They form closed loops around each wire, with the direction of the magnetic field lines determined by the right-hand rule. The magnetic field lines around Wire A and Wire B are in the same direction, creating a magnetic field that is stronger between the wires and weaker outside of them.

How Magnetic Field Lines are Formed Between Two Parallel Wires

When two parallel wires carry currents in opposite directions, the magnetic field lines between them behave differently. Let’s consider Wire A carrying current in the upward direction and Wire B carrying current in the downward direction.

At any point between the two wires, the magnetic field produced by Wire A is in one direction, while the magnetic field produced by Wire B is in the opposite direction. As a result, the magnetic field lines between the wires are attracted towards each other, creating a region of higher magnetic field intensity.

If the currents in Wire A and Wire B are equal, the magnetic field lines between the wires will be straight and parallel. The magnetic field lines will be closer together, indicating a stronger magnetic field between the wires. This is known as an attractive magnetic field.

On the other hand, if the currents in Wire A and Wire B are not equal, the magnetic field lines between the wires will be slightly curved. The magnetic field lines will be farther apart, indicating a weaker magnetic field between the wires. This is due to the imbalance in the magnetic forces exerted by the currents in the wires.

It is important to note that outside the region between the wires, the magnetic field lines follow the same circular pattern as explained earlier. The magnetic field lines around each wire are still circular and concentric, but their direction is opposite to the magnetic field lines between the wires.

The Role of Current in Magnetic Fields

When it comes to understanding magnetic fields, one important factor to consider is the role of current. Current refers to the flow of electric charge, typically in the form of electrons, through a conductor. In the context of magnetic fields, the presence of current can have a significant impact on the strength and direction of the magnetic field.

The effect of current on the magnetic field between two parallel wires

Let’s start by exploring the effect of current on the magnetic field between two parallel wires. According to Ampere’s law and the Biot-Savart law, the magnetic field produced by a current-carrying wire can be determined by the following equation:

$B = frac{{mu_0 cdot I}}{{2 pi cdot r}}$

Where: – B represents the magnetic field strength – (mu_0) is the permeability of free space (a constant value) – I is the current flowing through the wire – r is the distance from the wire

Now, imagine we have two parallel wires carrying currents in the same direction. The magnetic field lines produced by each wire will interact with each other, resulting in a combined magnetic field between the wires. The magnetic field lines will be circular around each wire, and the direction of the magnetic field will be perpendicular to the plane formed by the wires.

To understand this concept better, let’s consider an example. Suppose we have two parallel wires, each carrying a current of 2 Amperes. The distance between the wires is 0.5 meters. Using the formula mentioned earlier, we can calculate the magnetic field strength at a point between the wires:

$B = frac{{mu_0 cdot I}}{{2 pi cdot r}}$

$B = frac{{4 pi times 10^{-7} cdot 2}}{{2 pi cdot 0.5}}$

$B = 4 times 10^{-7} , T$

Therefore, the magnetic field strength between the two parallel wires is 4 x 10^-7 Tesla.

The difference in magnetic fields when current is in the same direction vs opposite direction

Now, let’s explore the difference in magnetic fields when the current in the wires is in the same direction versus the opposite direction.

When the currents in the wires are in the same direction, the magnetic fields produced by each wire reinforce each other. This means that the magnetic field between the wires will be stronger compared to the case when the currents are in opposite directions.

To illustrate this, let’s consider another example. Suppose we have two parallel wires, each carrying a current of 3 Amperes. The distance between the wires is 0.8 meters. Using the same formula as before, we can calculate the magnetic field strength at a point between the wires:

$B = frac{{mu_0 cdot I}}{{2 pi cdot r}}$

$B = frac{{4 pi times 10^{-7} cdot 3}}{{2 pi cdot 0.8}}$

$B = 5 times 10^{-7} , T$

Now, let’s consider the case when the currents in the wires are in opposite directions. In this scenario, the magnetic fields produced by each wire will partially cancel each other out. As a result, the magnetic field between the wires will be weaker compared to the case when the currents are in the same direction.

To further illustrate this, let’s use the same example as before but with opposite currents. The two parallel wires still carry a current of 3 Amperes, and the distance between them remains at 0.8 meters. Using the formula, we can calculate the magnetic field strength at a point between the wires:

$B = frac{{mu_0 cdot I}}{{2 pi cdot r}}$

$B = frac{{4 pi times 10^{-7} cdot 3}}{{2 pi cdot 0.8}}$

$B = 5 times 10^{-7} , T$

As we can see, the magnetic field strength between the wires is the same regardless of the direction of the currents. This is because the cancellation of the magnetic fields produced by the wires results in a net magnetic field of zero between the wires.

Calculating the Magnetic Field Between Two Parallel Wires

When two current-carrying wires are placed parallel to each other, they produce a magnetic field. Understanding the strength and direction of this magnetic field is crucial in various applications, such as designing electrical circuits and electromagnets. To calculate the magnetic field between two parallel wires, we can use the combination of Ampere’s law and the Biot-Savart law.

The magnetic field is a vector quantity, which means it has both magnitude and direction. It is represented by the symbol ‘B‘. The magnetic field lines around a current-carrying wire form concentric circles, with the wire at the center. The direction of the magnetic field can be determined using the right-hand rule.

The formula for calculating the magnetic field between two parallel wires is given by:

$B = frac{{mu_0 cdot I_1 cdot I_2 cdot d}}{{2 cdot pi cdot r}}$

Where: – (B) is the magnetic field strength – (mu_0) is the permeability of free space ((mu_0 = 4pi times 10^{-7} , text{Tm/A})) – (I_1) and (I_2) are the currents flowing through the wires – (d) is the distance between the wires – (r) is the distance from the point of observation to the wire

Let’s understand how to use this formula step-by-step.

Step-by-step guide on how to use the formula

Determine the values of (I_1), (I_2), (d), and (r) for the given problem. Make sure to use consistent units for all the variables.
Substitute the values into the formula:

$B = frac{{4pi times 10^{-7} , text{Tm/A} cdot I_1 cdot I_2 cdot d}}{{2 cdot pi cdot r}}$

Simplify the equation by canceling out the common factors:

$B = frac{{2 times 10^{-7} cdot I_1 cdot I_2 cdot d}}{{r}}$

Calculate the numerical value of the magnetic field using the given values:

$B = frac{{2 times 10^{-7} cdot I_1 cdot I_2 cdot d}}{{r}}$

Pay attention to the direction of the magnetic field. The magnetic field lines produced by each wire will be in the opposite direction, resulting in an attractive force between the wires.

Now, let’s work through an example to illustrate the calculation of the magnetic field between two parallel wires.

Example: Two parallel wires are placed 10 cm apart. Wire 1 carries a current of 2 A, while wire 2 carries a current of 3 A. Calculate the magnetic field at a point located 5 cm away from wire 1.

Solution: Given: (I_1 = 2 , text{A}) (I_2 = 3 , text{A}) (d = 10 , text{cm} = 0.1 , text{m}) (r = 5 , text{cm} = 0.05 , text{m})

Substituting the values into the formula:

$B = frac{{2 times 10^{-7} cdot 2 cdot 3 cdot 0.1}}{{0.05}}$

Simplifying the equation:

$B = 2 times 10^{-7} cdot 2 cdot 3 cdot 2 = 2.4 times 10^{-6} , text{T}$

Therefore, the magnetic field at a point located 5 cm away from wire 1 is (2.4 times 10^{-6} , text{T}).

By following these steps, you can calculate the magnetic field between two parallel wires. Remember to pay attention to the direction of the magnetic field and use consistent units throughout the calculation.

Force Between Two Parallel Wires

Explanation of the force between two parallel wires

The force between two parallel wires is a fascinating phenomenon that arises due to the interaction of their magnetic fields. When electric current flows through a wire, it creates a magnetic field around it. This magnetic field exerts a force on any other nearby wire carrying current. Let’s dive deeper into the explanation of this force.

To understand the force between two parallel wires, we need to consider the magnetic field produced by each wire and how they interact with each other. According to Ampere’s law and the Biot-Savart law, the magnetic field produced by a current-carrying wire can be calculated. The magnetic field lines around a wire form concentric circles, with the direction determined by the right-hand rule.

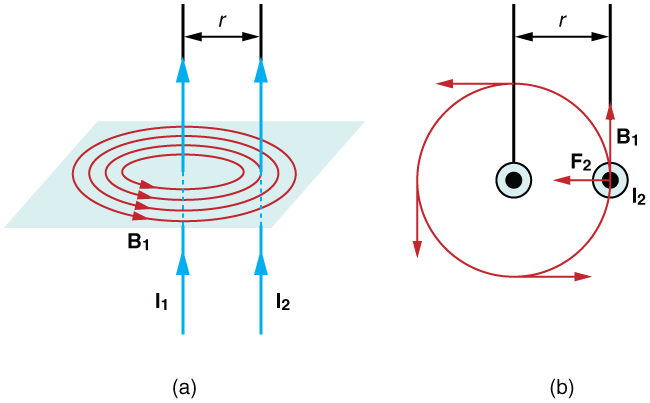
When two parallel wires are placed close to each other, their magnetic fields interact. If the currents in the wires are in the same direction, the magnetic field lines produced by both wires will be in the same direction. In this case, the wires will experience a magnetic force that is attractive, pulling them towards each other. On the other hand, if the currents are in opposite directions, the magnetic field lines will be in opposite directions, resulting in a repulsive force that pushes the wires apart.

The magnitude of the force between two parallel wires can be calculated using the following equation:

$F = frac{{mu_0 cdot I_1 cdot I_2 cdot L}}{{2 cdot pi cdot d}}$

Where: – (F) is the force between the wires – (mu_0) is the permeability of free space ((4pi times 10^{-7} , text{Tm/A})) – (I_1) and (I_2) are the currents in the wires – (L) is the length of the wires – (d) is the distance between the wires

Let’s consider an example to illustrate the calculation of the force between two parallel wires. Suppose we have two parallel wires, each carrying a current of 2 A. The length of each wire is 0.5 m, and the distance between them is 0.1 m. Using the formula mentioned earlier, we can calculate the force:

$F = frac{{4pi times 10^{-7} , text{Tm/A} cdot 2 , text{A} cdot 2 , text{A} cdot 0.5 , text{m}}}{{2 cdot pi cdot 0.1 , text{m}}} = 0.04 , text{N}$

Therefore, the force between the two parallel wires is 0.04 N.

How the magnetic field affects the force between two parallel wires

The magnetic field plays a crucial role in determining the force between two parallel wires. The direction and strength of the magnetic field influence the magnitude and direction of the force.

The magnetic field strength ((B)) at a point due to a current-carrying wire can be calculated using the following equation:

$B = frac{{mu_0 cdot I}}{{2 cdot pi cdot r}}$

Where: – (B) is the magnetic field strength – (mu_0) is the permeability of free space ((4pi times 10^{-7} , text{Tm/A})) – (I) is the current in the wire – (r) is the distance from the wire

The magnetic field strength is inversely proportional to the distance from the wire. As the distance increases, the magnetic field strength decreases.

When two parallel wires are close to each other, the magnetic field produced by one wire exerts a force on the other wire. The force is directly proportional to the product of the currents in the wires and the magnetic field strength. Additionally, the force is inversely proportional to the distance between the wires.

To observe the effect of the magnetic field on the force between two parallel wires, let’s consider an example. Suppose we have two parallel wires, each carrying a current of 3 A. The distance between the wires is 0.2 m. If the magnetic field strength at a point due to one wire is 2 T, we can calculate the force using the formula:

Therefore, the force between the two parallel wires is 3 N.

Practical Applications of Magnetic Fields Between Two Parallel Wires

Magnetic Field Between Two Parallel Wires — Image by OpenStax – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY 4.0.

Everyday Applications of Magnetic Fields Between Two Parallel Wires

Magnetic fields between two parallel wires have a wide range of everyday applications that we encounter in our daily lives. Let’s explore some of these practical applications:

Electromagnets: Electromagnets are devices that use the magnetic fields generated by current-carrying wires to produce a magnetic force. They are commonly used in various applications such as doorbells, speakers, and MRI machines. By controlling the current flowing through the wires, we can manipulate the strength and direction of the magnetic field, allowing us to create powerful electromagnets for different purposes.
Electric Motors: Electric motors rely on the interaction between magnetic fields and current-carrying wires to convert electrical energy into mechanical energy. When a current flows through the wires in the motor, it creates a magnetic field that interacts with the magnetic field produced by a permanent magnet. This interaction generates a force that causes the motor to rotate, enabling it to perform tasks such as powering appliances, vehicles, and industrial machinery.
Transformers: Transformers are essential devices used to transfer electrical energy between different circuits. They work based on the principle of magnetic induction between two parallel wires. By varying the number of turns in the wires, transformers can step up or step down the voltage of an alternating current (AC) signal. This allows for efficient transmission of electricity over long distances and enables us to use different voltage levels for various applications, such as in power distribution systems and electronic devices.
Induction Cooktops: Induction cooktops utilize magnetic fields between two parallel wires to generate heat directly in the cooking vessel. The cooktop contains a coil of wire through which an alternating current passes, creating a changing magnetic field. When a compatible cooking vessel, such as a ferromagnetic pot or pan, is placed on the cooktop, the magnetic field induces electric currents within the vessel. These currents generate heat due to resistance, heating up the cooking surface and allowing for efficient and precise cooking.

The Role of Magnetic Fields in Technology and Industry

Magnetic fields play a crucial role in various technological and industrial applications. Let’s delve into some of these roles:

Magnetic Field Sensing: Magnetic field sensors are widely used in industries to detect and measure magnetic fields. These sensors are essential in applications such as navigation systems, robotics, and magnetic resonance imaging (MRI) machines. By accurately sensing and measuring magnetic fields, these sensors enable precise control and monitoring of various processes and systems.
Magnetic Levitation: Magnetic levitation, also known as maglev, is a technology that uses magnetic fields to suspend and propel objects, such as trains and vehicles, without physical contact. By utilizing the repulsive or attractive forces between magnets and current-carrying wires, maglev systems can achieve high speeds, reduce friction, and provide a smooth and efficient mode of transportation.
Magnetic Data Storage: Magnetic fields are extensively used in data storage devices, such as hard disk drives (HDDs) and magnetic tapes. These devices utilize the magnetic properties of materials to store and retrieve digital information. By applying magnetic fields to tiny regions on the storage medium, data can be encoded and stored magnetically, allowing for high-capacity and non-volatile storage solutions.
Magnetic Particle Inspection: Magnetic particle inspection is a non-destructive testing method used in industries to detect surface and near-surface defects in materials. By applying a magnetic field to the material being inspected and using magnetic particles, defects such as cracks and discontinuities can be visualized. This technique is widely employed in industries such as aerospace, automotive, and manufacturing to ensure the quality and integrity of critical components.

Frequently Asked Questions

Q1: Why do two parallel current-carrying wires attract each other?

A1: Two parallel current-carrying wires attract each other due to the interaction of their magnetic fields. The magnetic field produced by one wire induces a magnetic field in the other wire, resulting in an attractive force between them.

Q2: What is the net magnetic field between two parallel wires?

A2: The net magnetic field between two parallel wires is the vector sum of the individual magnetic fields produced by each wire. It can be calculated using the Biot-Savart law or Ampere’s law, depending on the specific configuration.

Q3: What is the direction of the magnetic field between two parallel wires?

A3: The direction of the magnetic field between two parallel wires depends on the direction of the current flowing through the wires. The magnetic field forms concentric circles around each wire and is in the same direction for both wires.

Q4: How to find the magnetic field between two parallel wires?

A4: The magnetic field between two parallel wires can be found using the Biot-Savart law or Ampere’s law. These laws involve integrating the contributions of infinitesimally small current elements along the wires to determine the magnetic field at a specific point.

Q5: What is the magnetic field at a point midway between two parallel long wires?

A5: The magnetic field at a point midway between two parallel long wires carrying current in the same direction is zero. This is because the magnetic fields produced by the wires cancel each other out at that specific point.

Q6: What is the magnetic field strength between two parallel wires?

A6: The magnetic field strength between two parallel wires depends on the distance between the wires, the current flowing through them, and the permeability of the medium. It can be calculated using the Biot-Savart law or Ampere’s law.

Q7: What is the direction of the force between two parallel wires?

A7: The force between two parallel wires carrying current depends on the direction of the currents. If the currents are in the same direction, the wires attract each other. If the currents are in opposite directions, the wires repel each other.

Q8: What is the magnetic field around two parallel wires?

A8: The magnetic field around two parallel wires forms concentric circles around each wire. The field lines are perpendicular to the wires and are in the same direction for both wires.

Q9: What is the magnetic field midway between two parallel current-carrying wires?

A9: The magnetic field midway between two parallel current-carrying wires depends on the distance between the wires, the currents flowing through them, and the permeability of the medium. It can be calculated using the Biot-Savart law or Ampere’s law.

Q10: What is the magnetic field between two parallel wires carrying current in the same direction?

A10: The magnetic field between two parallel wires carrying current in the same direction is directly proportional to the current and inversely proportional to the distance between the wires. It can be calculated using the Biot-Savart law or Ampere’s law.

Also Read:

Keerthi Murthi

I am Keerthi K Murthy, I have completed post graduation in Physics, with the specialization in the field of solid state physics. I have always consider physics as a fundamental subject which is connected to our daily life. Being a science student I enjoy exploring new things in physics. As a writer my goal is to reach the readers with the simplified manner through my articles.

Key Takeaways

Understanding Magnetic Fields

Definition and Explanation of Magnetic Fields

Magnetic Field Between Two Parallel Wires

Explanation of the magnetic field between two parallel wires

Factors affecting the magnetic field between two parallel wires

Magnetic Field Direction and Strength

Understanding the direction of the magnetic field between two parallel wires

Determining the strength of the magnetic field between two parallel wires

Magnetic Field Lines of Two Parallel Wires

Explanation of Magnetic Field Lines

How Magnetic Field Lines are Formed Between Two Parallel Wires

The Role of Current in Magnetic Fields

The effect of current on the magnetic field between two parallel wires

The difference in magnetic fields when current is in the same direction vs opposite direction

Calculating the Magnetic Field Between Two Parallel Wires

Step-by-step guide on how to use the formula

Force Between Two Parallel Wires

Explanation of the force between two parallel wires

How the magnetic field affects the force between two parallel wires

Practical Applications of Magnetic Fields Between Two Parallel Wires

Everyday Applications of Magnetic Fields Between Two Parallel Wires

The Role of Magnetic Fields in Technology and Industry

Frequently Asked Questions

Q1: Why do two parallel current-carrying wires attract each other?

Q2: What is the net magnetic field between two parallel wires?

Q3: What is the direction of the magnetic field between two parallel wires?

Q4: How to find the magnetic field between two parallel wires?

Q5: What is the magnetic field at a point midway between two parallel long wires?

Q6: What is the magnetic field strength between two parallel wires?

Q7: What is the direction of the force between two parallel wires?

Q8: What is the magnetic field around two parallel wires?

Q9: What is the magnetic field midway between two parallel current-carrying wires?

Q10: What is the magnetic field between two parallel wires carrying current in the same direction?

Hi Fellow Reader,