How to Find Energy Levels in a Quantum Dot: A Comprehensive Guide

Quantum dots are fascinating nanostructures that exhibit unique properties due to their small size and quantum confinement. One of the key aspects of understanding and studying quantum dots is the determination of their energy levels. By finding the energy levels in a quantum dot, we can gain insights into the behavior of electrons within the dot and how these energy levels affect the overall properties of the system. In this blog post, we will explore the concept of energy levels in quantum dots, delve into the process of finding these energy levels, and discuss their practical applications in quantum chemistry.

Determining Energy Levels in Quantum Dots

The Concept of Quantum Numbers

To understand energy levels in quantum dots, we must first grasp the concept of quantum numbers. Quantum numbers describe the unique quantum states of electrons within an atom or a nanostructure like a quantum dot. In the case of quantum dots, the relevant quantum numbers are similar to those used in atomic physics, such as the principal quantum number (n), azimuthal quantum number (l), magnetic quantum number (m), and spin quantum number (s).

The Relationship between Quantum Numbers and Energy Levels

How to find energy levels in a quantum dot — Image by Jpailee – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

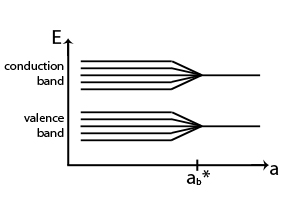
Each combination of quantum numbers corresponds to a specific energy level in a quantum dot. The principal quantum number (n) determines the energy level’s size and the distance of the electron from the nucleus. The azimuthal quantum number (l) determines the shape of the electron’s probability distribution, while the magnetic quantum number (m) determines its orientation in space. Finally, the spin quantum number (s) describes the electron’s intrinsic spin.

The Process of Finding Energy Levels Given Quantum Numbers

To find the energy levels in a quantum dot, we need to solve the wave equation for the system. The wave equation, also known as the Schrödinger equation, describes the behavior of quantum particles, including electrons, in a given potential energy field. Solving this equation yields the wave functions and corresponding energies for the quantum dot system.

The wave equation for a quantum dot typically involves solving a set of differential equations, which can be quite complex. However, there are various numerical and analytical methods available to simplify these calculations and obtain the energy levels.

Practical Application: Calculating Energy Levels in Quantum Dots

Step-by-step Guide on How to Calculate Energy Levels

Let’s walk through a step-by-step guide on how to calculate energy levels in a quantum dot:

Define the potential energy profile of the quantum dot. This profile describes how the energy of the electron changes within the dot as a function of position.
Set up and solve the wave equation for the quantum dot system, taking into account the boundary conditions and constraints.
Use numerical or analytical methods to solve the resulting differential equations and obtain the wave functions.
Normalize the wave functions to determine the probability distribution of the electron within the quantum dot.
Calculate the energies associated with each wave function by applying the appropriate mathematical operator to the wave functions. These energies correspond to the energy levels of the quantum dot.

Worked-out Examples of Energy Level Calculations

Let’s consider a specific example to illustrate the calculation of energy levels in a quantum dot. Suppose we have a spherical quantum dot with a parabolic confinement potential. By solving the wave equation for this system and applying the appropriate mathematical operators, we can obtain the energy levels and corresponding wave functions. These energy levels dictate the behavior and properties of electrons within the quantum dot.

Common Challenges and Solutions in Calculating Energy Levels

Calculating energy levels in quantum dots can present some challenges, especially for complex systems or when considering electron-electron interactions. One common challenge is solving the wave equation analytically, as it may not always be feasible. In such cases, numerical methods like the finite element method or the finite difference method can provide accurate solutions.

Another challenge arises when including the effects of electron-electron interactions, which can significantly influence the energy levels in quantum dots. Various approximation methods, such as the Hartree-Fock method or density functional theory, can be employed to account for these interactions and obtain more realistic energy level calculations.

The Role of Energy Levels in Quantum Chemistry

Understanding Quantum Energy Levels in Chemistry

Energy levels play a crucial role in quantum chemistry as they determine the electronic structure and behavior of atoms, molecules, and nanostructures. By studying the energy levels in quantum dots, we can gain insights into the electronic properties of these nanostructures and how they interact with light and other particles.

The Connection between Energy Levels and the Behavior of Electrons

The energy levels in a quantum dot dictate the possible states and behavior of electrons within the dot. Electrons occupy these energy levels in accordance with the Pauli exclusion principle, filling the levels from lower to higher energy. The distribution of electrons among the energy levels influences the dot’s conductivity, optical properties, and quantum confinement effects.

The Impact of Energy Levels on the Properties of Atoms

The energy levels in a quantum dot have a direct impact on its optical properties, including absorption and emission spectra. The energy difference between different levels determines the wavelengths of light that a quantum dot can absorb or emit, making it useful for applications such as optoelectronics and quantum information processing.

Furthermore, energy level calculations provide valuable information about the electronic states and excitations in quantum dots, offering insights into the material’s electronic structure and its potential applications in various fields, including catalysis, sensing, and energy conversion.

Determining energy levels in quantum dots is a fundamental aspect of understanding the behavior and properties of these nanostructures. By considering the quantum numbers, solving the wave equation, and calculating the corresponding energies, we can gain valuable insights into the electronic structure, optical properties, and behavior of electrons in quantum dots. These energy level calculations have practical applications in quantum chemistry and pave the way for advancements in fields such as nanotechnology, optoelectronics, and materials science.

Numerical Problems on How to Find Energy Levels in a Quantum Dot

Problem 1:

A quantum dot with a potential energy function given by:

$[ V(x) = \begin{cases}0 & 0 \leq x \leq a \V_0 & x > a\end{cases}]$

has a width of $a = 10$ nm and a barrier height of $V_0 = 2$ eV. Calculate the energy levels of the quantum dot.

Solution:

The energy levels of a quantum dot can be found by solving the time-independent Schrödinger equation:

$\hat{H}\psi(x) = E\psi(x)$

where $\hat{H}$ is the Hamiltonian operator, $\psi(x$ ) is the wave function, $E$ is the energy, and $x$ is the position.

For the given potential energy function, the Hamiltonian operator can be written as:

$\hat{H} = -\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} + V(x)$

Substituting the potential energy function into the Hamiltonian operator, we have:

$[ \hat{H} = -\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} + \begin{cases}0 & 0 \leq x \leq a \V_0 & x > a\end{cases}]$

To solve the Schrödinger equation, we can split it into two regions: the region $0 \leq x \leq a$ and the region $x > a$ .

In the region $0 \leq x \leq a$ , the potential energy is zero, so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) = E \psi(x) \quad \text{for } 0 \leq x \leq a$

Simplifying the equation, we get:

$\frac{{d^2}}{{dx^2}} \psi(x) = -\frac{{2mE}}{{\hbar^2}} \psi(x) \quad \text{for } 0 \leq x \leq a$

The general solution to this differential equation is:

$\psi(x) = A \sin(kx) + B \cos(kx)$

where $A$ and $B$ are constants to be determined, and $k$ is given by:

$k = \sqrt{\frac{{2mE}}{{\hbar^2}}}$

In the region $x > a$ , the potential energy is $V_0$ , so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) + V_0 \psi(x) = E \psi(x) \quad \text{for } x > a$

Simplifying the equation, we get:

$\frac{{d^2}}{{dx^2}} \psi(x) = -\frac{{2m}}{{\hbar^2}} (E - V_0) \psi(x) \quad \text{for } x > a$

The general solution to this differential equation is:

$\psi(x) = C \sin(qx) + D \cos(qx)$

where $C$ and $D$ are constants to be determined, and $q$ is given by:

$q = \sqrt{\frac{{2m}}{{\hbar^2}} (E - V_0)}$

Applying the boundary conditions, we have:

At $x = 0$ , the wave function must be finite, so $B = 0$ .
At $x = a$ , the wave function and its derivative must be continuous, so:

$A \sin(ka) = C \sin(qa) + D \cos(qa) \quad \text{(1)}$
$kA \cos(ka) = qC \cos(qa) - qD \sin(qa) \quad \text{(2)}$

To simplify the equations, we can rewrite them as:

$\tan(ka) = \frac{{qC + D}}{{C - qD}} \quad \text{(3)}$

The energy levels can be found by solving equation $3) for different values of \( E$ .

Problem 2:

Consider a quantum dot with a potential energy function given by:

$[ V(x) = \begin{cases}0 & 0 \leq x \leq a \\frac{{V_0}}{{2}} & x = a \V_0 & x > a\end{cases}]$

where $a = 5$ nm and $V_0 = 1$ eV. Determine the energy levels of the quantum dot.

Solution:

To find the energy levels, we need to solve the time-independent Schrödinger equation:

$\hat{H}\psi(x) = E\psi(x)$

where $\hat{H}$ is the Hamiltonian operator, $\psi(x)$ is the wave function, $E$ is the energy, and $x$ is the position.

For the given potential energy function, the Hamiltonian operator can be written as:

$\hat{H} = -\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} + V(x)$

Substituting the potential energy function into the Hamiltonian operator, we have:

$[ \hat{H} = -\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} + \begin{cases}0 & 0 \leq x \leq a \\frac{{V_0}}{{2}} & x = a \V_0 & x > a\end{cases}]$

To solve the Schrödinger equation, we can split it into three regions: the region $0 \leq x \leq a$ , the region $x = a$ , and the region $x > a$ .

In the region $0 \leq x \leq a$ , the potential energy is zero, so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) = E \psi(x) \quad \text{for } 0 \leq x \leq a$

Simplifying the equation, we get:

$\frac{{d^2}}{{dx^2}} \psi(x) = -\frac{{2mE}}{{\hbar^2}} \psi(x) \quad \text{for } 0 \leq x \leq a$

The general solution to this differential equation is:

$\psi(x) = A \sin(kx) + B \cos(kx)$

where $A$ and $B$ are constants to be determined, and $k$ is given by:

$k = \sqrt{\frac{{2mE}}{{\hbar^2}}}$

In the region $x = a$ , the potential energy is $\frac{{V_0}}{{2}}$ , so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) + \frac{{V_0}}{{2}} \psi(x) = E \psi(x) \quad \text{for } x = a$

Since the potential energy is constant in this region, the wave function must also be constant, so:

$\psi(x) = C \quad \text{for } x = a$

In the region $x > a$ , the potential energy is $V_0$ , so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) + V_0 \psi(x) = E \psi(x) \quad \text{for } x > a$

Simplifying the equation, we get:

$\frac{{d^2}}{{dx^2}} \psi(x) = -\frac{{2m}}{{\hbar^2}} (E - V_0) \psi(x) \quad \text{for } x > a$

The general solution to this differential equation is:

$\psi(x) = D \sin(qx) + E \cos(qx)$

where $D$ and $E$ are constants to be determined, and $q$ is given by:

$q = \sqrt{\frac{{2m}}{{\hbar^2}} (E - V_0)}$

Applying the boundary conditions, we have:

At $x = 0$ , the wave function must be finite, so $B = 0$ .
At $x = a$ , the wave function and its derivative must be continuous, so:

$A \sin(ka) + B \cos(ka) = C \quad \text{(1)}$
$kA \cos(ka) = D \sin(qa) + E \cos(qa) \quad \text{(2)}$

To simplify the equations, we can rewrite them as:

$\tan(ka) = \frac{{D \sin(qa) + E \cos(qa)}}{{C}} \quad \text{(3)}$

The energy levels can be found by solving equation $3) for different values of \( E$ .

Problem 3:

A quantum dot is characterized by a potential energy function given by:

$[ V(x) = \begin{cases}0 & 0 \leq x \leq a \V_0 & a < x \leq 2a \0 & x > 2a\end{cases}]$

where $a = 8$ nm and $V_0 = 3$ eV. Determine the energy levels of the quantum dot.

Solution:

To find the energy levels, we need to solve the time-independent Schrödinger equation:

$\hat{H}\psi(x) = E\psi(x)$

where $\hat{H}$ is the Hamiltonian operator, $\psi(x$ ) is the wave function, $E$ is the energy, and $x$ is the position.

For the given potential energy function, the Hamiltonian operator can be written as:

$\hat{H} = -\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} + V(x)$

Substituting the potential energy function into the Hamiltonian operator, we have:

$[ \hat{H} = -\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} + \begin{cases}0 & 0 \leq x \leq a \V_0 & a < x \leq 2a \0 & x > 2a\end{cases}]$

To solve the Schrödinger equation, we can split it into three regions: the region $0 \leq x \leq a$ , the region $a < x \leq 2a$ , and the region $x > 2a$ .

In the region $0 \leq x \leq a$ , the potential energy is zero, so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) = E \psi(x) \quad \text{for } 0 \leq x \leq a$

Simplifying the equation, we get:

$\frac{{d^2}}{{dx^2}} \psi(x) = -\frac{{2mE}}{{\hbar^2}} \psi(x) \quad \text{for } 0 \leq x \leq a$

The general solution to this differential equation is:

$\psi(x) = A \sin(kx) + B \cos(kx)$

where $A$ and $B$ are constants to be determined, and $k$ is given by:

$k = \sqrt{\frac{{2mE}}{{\hbar^2}}}$

In the region $a < x \leq 2a$ , the potential energy is $V_0$ , so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) + V_0 \psi(x) = E \psi(x) \quad \text{for } a < x \leq 2a$

Simplifying the equation, we get:

$\frac{{d^2}}{{dx^2}} \psi(x) = -\frac{{2m}}{{\hbar^2}} (E - V_0) \psi(x) \quad \text{for } a < x \leq 2a$

The general solution to this differential equation is:

$\psi(x) = C \sin(qx) + D \cos(qx)$

where $C$ and $D$ are constants to be determined, and $q$ is given by:

$q = \sqrt{\frac{{2m}}{{\hbar^2}} (E - V_0)}$

In the region $x > 2a$ , the potential energy is zero again, so the Schrödinger equation becomes:

$-\frac{{\hbar^2}}{{2m}} \frac{{d^2}}{{dx^2}} \psi(x) = E \psi(x) \quad \text{for } x > 2a$

Simplifying the equation, we get:

$\frac{{d^2}}{{dx^2}} \psi(x) = -\frac{{2mE}}{{\hbar^2}} \psi(x) \quad \text{for } x > 2a$

The general solution to this differential equation is:

$\psi(x) = F \sin(k'x) + G \cos(k'x)$

where $F$ and $G$ are constants to be determined, and $k'$ is given by:

$k' = \sqrt{\frac{{2mE}}{{\hbar^2}}}$

Applying the boundary conditions, we have:

At $x = 0$ , the wave function must be finite, so $B = 0$ .
At $x = a$ , the wave function and its derivative must be continuous, so:

$A \sin(ka) = C \sin(qa) + D \cos(qa) \quad \text{(1)}$
$kA \cos(ka) = qC \cos(qa) - qD \sin(qa) \quad \text{(2)}$

At $x = 2a$ , the wave function and its derivative must be continuous, so:

$C \sin(qa) + D \cos(qa) = F \sin(k'a) + G \cos(k'a) \quad \text{(3)}$
$qC \cos(qa) - qD \sin(qa) = k'F \cos(k'a) - k'G \sin(k'a) \quad \text{(4)}$

To simplify the equations, we can rewrite them as:

$\tan(ka) = \frac{{qC + D}}{{C - qD}} \quad \text{(5)}$
$\tan(k'a) = \frac{{k'F + G}}{{F - k'G}} \quad \text{(6)}$

The energy levels can be found by solving equations $5) and (6) for different values of \( E$ .

Also Read:

TechieScience Core SME

The TechieScience Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the TechieScience.com website.

All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.

techiescience.com