How to Find Angular Momentum of a System: A Comprehensive Guide

How to Find Angular Momentum of a System

Angular momentum is a fundamental concept in physics that describes the rotational motion of a system. It plays a crucial role in understanding rotational dynamics, conservation laws, and many other areas of physics. In this blog post, we will explore how to find the angular momentum of a system, step by step, along with relevant formulas and examples.

Understanding the Concept of Angular Momentum

Angular momentum can be defined as the measure of an object’s tendency to continue rotating about a given axis. It depends on two main factors: the moment of inertia and the angular velocity of the object. Think of it as the rotational equivalent of linear momentum.

The moment of inertia, represented by the symbol I, quantifies an object’s resistance to changes in rotational motion. It depends on the mass distribution of the object and the axis of rotation. The larger the moment of inertia, the more difficult it is to change the object’s rotational motion.

On the other hand, angular velocity, denoted by the symbol ω, measures how fast an object rotates about a given axis. It is defined as the rate of change of angular displacement with respect to time. It is usually measured in radians per second (rad/s).

The Mathematical Formula for Angular Momentum

The mathematical formula for angular momentum is given by:

$L = I cdot omega$

Where:
– L represents the angular momentum of the object,
– I is the moment of inertia of the object, and
– ω is the angular velocity of the object.

Steps to Calculate Angular Momentum

Now, let’s go through the steps to calculate the angular momentum of a system.

Identifying the Variables in the System: First, you need to identify the variables involved in the system. This includes the moment of inertia (I) and the angular velocity (ω) of the object or objects in the system.
Applying the Angular Momentum Formula: Once you have identified the variables, you can proceed to calculate the angular momentum using the formula L = I * ω. Plug in the values of the moment of inertia and the angular velocity into the formula.
Worked-out Examples of Calculating Angular Momentum: To better understand the concept, let’s work through a couple of examples.

Example 1: Consider a rotating disc with a moment of inertia of 2 kg·m² and an angular velocity of 4 rad/s. Using the formula L = I * ω, we can calculate the angular momentum as follows:

$L = 2 , text{kg} cdot text{m}^2 times 4 , text{rad/s} = 8 , text{kg} cdot text{m}^2/text{s}$

Example 2: Suppose a particle with a moment of inertia of 0.5 kg·m² is rotating at an angular velocity of 6 rad/s. The angular momentum can be calculated as:

$L = 0.5 , text{kg} cdot text{m}^2 times 6 , text{rad/s} = 3 , text{kg} cdot text{m}^2/text{s}$

These examples demonstrate how to calculate the angular momentum using the formula and given values.

Conservation of Angular Momentum

The principle of conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant. This principle is similar to the conservation of linear momentum.

The conservation of angular momentum can be understood using the example of a spinning ice skater. When an ice skater pulls their arms closer to their body, their moment of inertia decreases. According to the law of conservation of angular momentum, the decrease in moment of inertia results in an increase in angular velocity, enabling the skater to rotate faster.

How to Determine if Angular Momentum is Conserved

How to Find Angular Momentum of a System — Image by Jacopo Bertolotti – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

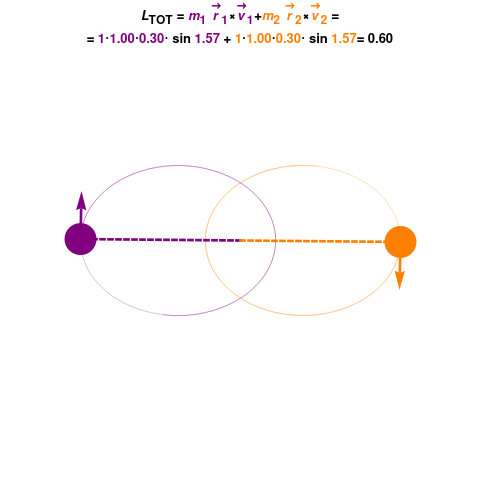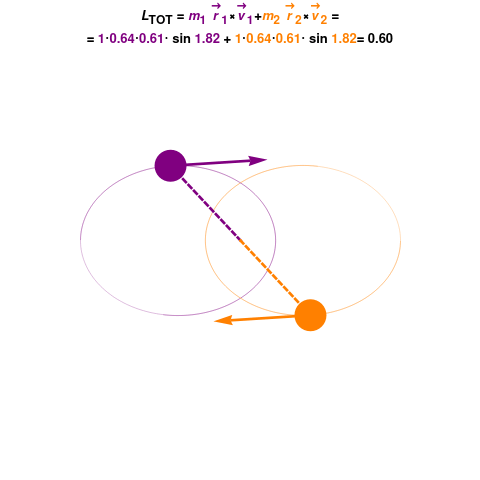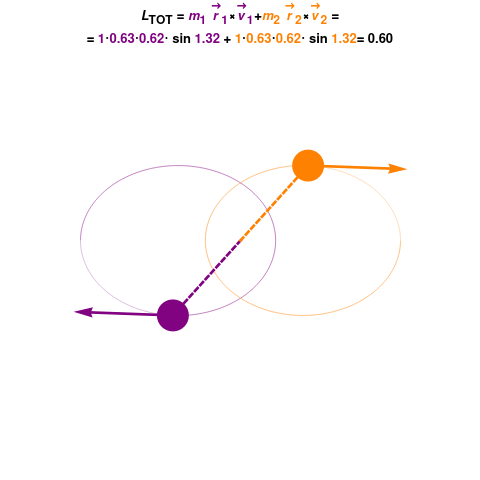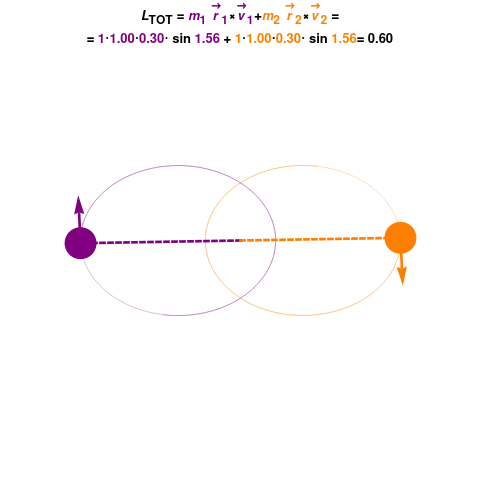
To determine if angular momentum is conserved in a system, you need to examine whether there are any external torques acting upon it. If there are no external torques, the angular momentum will be conserved.

In practice, you can analyze the system for any external forces or moments acting on it. If there are none, you can conclude that the angular momentum is conserved.

Examples of Conservation of Angular Momentum in Real Life

Image by Olivier Cleynen – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

Conservation of angular momentum can be observed in various real-life scenarios. Here are a few examples:

Ice skaters: As mentioned earlier, when ice skaters pull their arms closer to their bodies, their moment of inertia decreases, resulting in an increase in angular velocity. This conservation of angular momentum allows them to perform faster spins.
Diving: Divers often tuck their bodies into a tight ball during somersaults. By reducing their moment of inertia, they increase their angular velocity, making it easier to complete multiple rotations before entering the water.
Planetary motion: The conservation of angular momentum is crucial in understanding the motion of planets and satellites. As a planet moves closer to the Sun in its elliptical orbit, its moment of inertia decreases, causing an increase in angular velocity to maintain angular momentum.

The conservation of angular momentum is a fundamental concept that helps explain the behavior of rotating objects and systems.

Numerical Problems on How to Find Angular Momentum of a System

Problem 1:

A system consists of two particles with masses of 0.5 kg and 1 kg, respectively. The first particle has a velocity of 2 m/s, while the second particle has a velocity of 3 m/s. Calculate the angular momentum of the system.

Solution:
The angular momentum of a particle is given by the formula:
$L = mvr$
where:
$L$ = angular momentum,
$m$ = mass of the particle,
$v$ = velocity of the particle,
$r$ = perpendicular distance from the particle to the axis of rotation.

Let’s assume the perpendicular distance from the particles to the axis of rotation is 1 meter.

For the first particle:
$L_1 = (0.5 , text{kg})(2 , text{m/s})(1 , text{m}) = 1 , text{kg m}^2/text{s}$

For the second particle:
$L_2 = (1 , text{kg})(3 , text{m/s})(1 , text{m}) = 3 , text{kg m}^2/text{s}$

The total angular momentum of the system is the sum of the angular momenta of the particles:
$L_{text{system}} = L_1 + L_2 = 1 , text{kg m}^2/text{s} + 3 , text{kg m}^2/text{s} = 4 , text{kg m}^2/text{s}$

Therefore, the angular momentum of the system is 4 kg m²/s.

Problem 2:

A rotating system consists of a disk with a mass of 2 kg and a radius of 0.5 m. The disk is rotating at a speed of 10 rad/s. Calculate the angular momentum of the system.

Solution:
The angular momentum of a rotating object is given by the formula:
$L = I omega$
where:
$L$ = angular momentum,
$I$ = moment of inertia of the object,
$omega$ = angular velocity of the object.

The moment of inertia of a disk rotating about its axis is given by the formula:
$I = frac{1}{2} m r^2$
where:
$m$ = mass of the disk,
$r$ = radius of the disk.

Substituting the given values:
$I = frac{1}{2} (2 , text{kg}) (0.5 , text{m})^2 = 0.5 , text{kg m}^2$

Now, we can calculate the angular momentum:
$L = (0.5 , text{kg m}^2) (10 , text{rad/s}) = 5 , text{kg m}^2/text{s}$

Therefore, the angular momentum of the system is 5 kg m²/s.

Problem 3:

A system is composed of three particles with masses of 2 kg, 3 kg, and 4 kg, respectively. The particles have velocities of 3 m/s, 4 m/s, and 5 m/s, respectively. The perpendicular distances of the particles from the axis of rotation are 2 m, 3 m, and 4 m, respectively. Calculate the angular momentum of the system.

For the first particle:
$L_1 = (2 , text{kg})(3 , text{m/s})(2 , text{m}) = 12 , text{kg m}^2/text{s}$

For the second particle:
$L_2 = (3 , text{kg})(4 , text{m/s})(3 , text{m}) = 36 , text{kg m}^2/text{s}$

For the third particle:
$L_3 = (4 , text{kg})(5 , text{m/s})(4 , text{m}) = 80 , text{kg m}^2/text{s}$

The total angular momentum of the system is the sum of the angular momenta of the particles:
$L_{text{system}} = L_1 + L_2 + L_3 = 12 , text{kg m}^2/text{s} + 36 , text{kg m}^2/text{s} + 80 , text{kg m}^2/text{s} = 128 , text{kg m}^2/text{s}$

Therefore, the angular momentum of the system is 128 kg m²/s.

Also Read:

TechieScience Core SME

The TechieScience Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the TechieScience.com website.

All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.

techiescience.com